Cho tứ diện đều A B C D cạnh bằng a . Khoảng cách giữa hai đường thẳng A B và C D bằng
A. 3 a 2 .
B. a .
C. a 3 2 .
D. a 2 2 .
Cho tứ diện đều ABCD cạnh bằng a. Khoảng cách d giữa hai đường thẳng AD và BC là:
A . d = a 3 2
B . d = a 2 2
C . d = a 2 3
D . d = a 3 3
Đáp án B
Gọi O là trọng tâm ∆ABC
Kẻ AM ⊥ AC và MH ⊥ AD
Vì DABC là tứ diện đều => DO ⊥ (ABC)
Vì ∆ABC đều => AO = ![]()
Xét ∆DAO vuông tại O

Ta có: DO ⊥ BC và AM ⊥ BC
=> (DAM) ⊥ BC
=> MH ⊥ BC
Lại có MH ⊥ DA
=> MH = d(BC, DA)
Xét ∆DAM, ta có:
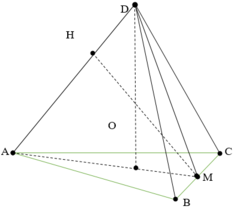
DO.AM = MH.AD
⇔ MH = a 2 2
⇔ d(BC, DA) = a 2 2
Cho tứ diện đều ABCD cạnh bằng a. Khoảng cách d giữa hai đường thẳng AD và BC là:
A. d = a 3 2
B. d = a 2 2
C. d = a 2 3
D. d = a 3 3
Đáp án B.
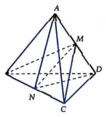
Gọi M,N lần lượt là trung điểm của AD và BC. Ta có ∆ A B D và ∆ A C D đều cạnh bằng a nên B M = C M = a 3 2 ⇒ ∆ M B C cân tại M và MN là đường cao của ∆ M B C ⇒ M N ⊥ B C
Tương tự, ∆ N A D cân tại N nên NM là đường cao của ∆ N A D ⇒ N M ⊥ A D
Suy ra MN là đoạn vuông góc cung của AD và BC.
Vậy d A D ; B C = M N = B M 2 - B C 2 2 = a 3 2 2 - a 2 2 = a 2 2
Cho tứ diện đều ABCD cạnh bằng a . Khoảng cách d giữa hai đường thẳng AD và BC là:
A. d = a 3 2
B. d = a 2 2
C. d = a 2 3
D. d = a 3 3
Cho tứ diện đều ABCD cạnh bằng a. Khoảng cách d giữa hai đường thẳng AD và BC là:
A . d = a 3 2
B . d = a 2 2
C . d = a 2 3
D . d = a 3 3
Đáp án B.
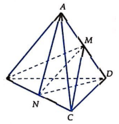
Gọi lần lượt là trung điểm của AD và BC. Ta có ∆ ABD và ∆ ACD đều cạnh bằng a nên
![]()
=> ∆ MBC cân tại M và MN là đường cao của ∆ MBC => MN ⊥ BC
Tương tự, ∆ NAD cân tại N nên NM là đường cao của ∆ NAD => NM ⊥ AD
Suy ra MN là đoạn vuông góc cung của AD và BC.
Vậy
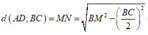
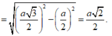
Cho tứ diện đều ABCD cạnh bằng a. Khoảng cách d giữa hai đường thẳng AD và BC là
A. d = a 3 2
B. d = a 2 2
C. d = a 2 3
D. d = a 3 3
Cho hình tứ diện đều ABCD cạnh bằng a, gọi d là khoảng cách giữa hai đường thẳng AB và CD .Tìm d
A. d(AB;CD)=a
B. d(AB;CD)=a/3
C. d(AB;CD)=a/2
D. d A B ; C D = a 2 2
Cho tứ diện ABCD có AC=AD=BC=BD, AB=a, CD= a 3 Khoảng cách giữa hai đường thẳng AB và CD bằng a . Tính khoảng cách h từ điểm cách đều 4 đỉnh A,B,C,D đến mỗi đỉnh đó
A. h = a 13 2
B. h = a 13 4
C. h = a 3 2
D. h = a 3 4
Cho tứ diện ABCD có A B = A D = B C = B D , A B = a , C D = a 30 . Khoảng cách giữa hai đường thẳng AB và CD bằng a. Tính khoảng cách h từ điểm cách đều 4 đỉnh A, B, C, D đến mỗi đỉnh đó.
A. h = a 13 2
B. h = a 13 4
C. h = a 3 2
D. h = a 3 4
Chọn B
Gọi I là trung điểm AB, J là trung điểm CD
Từ AC=AD=BC=BD =>IJ chính là đoạn vuông góc chung của 2 đường thẳng AB và CD
=> IJ = a
Gọi O là điểm cách đều 4 đỉnh => O là tâm mặt cầu ngoại tiếp tứ diện ABCD
=> O nằm trên IJ => Ta cần tính OA
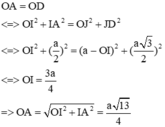
Ta có:
Hình hộp A B C D . A , B , C , D , có A B = A A , = A D = a và A , A B ⏜ = A , A D ⏜ = B A D ⏜ = 60 0 Khoảng cách giữa các đường thẳng chứa các cạnh đối diện của tứ diện A , A B D bằng