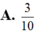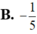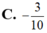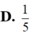Phần ảo của số phức z = -1 + i là
A. -i
B. 1
C. -1
D. i
Những câu hỏi liên quan
a) tìm phần ảo của số phức z2 , biết (1+i)z= 1/z
b) tìm mô-đun của số phức z biết 1/z = 1/2 + 1/2i
c) i + i2+ i3 +...... i100
d) 1+(1+i) +(1+ i)^2+(1+i)^3+..... (1+i)^20
a/\(\left(1+i\right)z=\frac{1}{z}\Leftrightarrow z^2\left(1+i\right)=1\Rightarrow z^2=\frac{1}{1+i}=\frac{1}{2}-\frac{1}{2}i\)
\(\Rightarrow\) Phần ảo là \(-\frac{1}{2}\)
b/\(\frac{1}{z}=\frac{1}{2}+\frac{1}{2}i\Rightarrow z=\frac{2}{1+i}\Rightarrow z=1-i\)
Phần ảo là -1
c/ Áp dụng công thức tổng CSN với \(u_1=i\) ; \(q=i\); \(n=100\)
\(i+i^2+...+i^{100}=i.\frac{i^{101}-1}{i-1}=\frac{i^{102}-i}{i-1}=\frac{\left(i^2\right)^{51}-i}{i-1}=\frac{-1-i}{i-1}=i\)
d/ Tương tự câu trên:
\(1+\left(1+i\right)+...+\left(1+i\right)^{20}=1+\left(1+i\right).\frac{\left(1+i\right)^{21}-1}{1+i-1}=-2048+i\)
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
5
z
+
i
2
-
i
z
+
1
. Gọ...
Đọc tiếp
Cho số phức z thỏa mãn 5 z + i = 2 - i z + 1 . Gọi a, b lần lượt là phần thực và phần ảo của số phức 1 + z + z 2 , tổng a+b bằng
A. 13
B. -5
C. 9
D. 5
Cho số phức z thỏa mãn
5
z
¯
+
i
2
-
i
z
+
1
. Gọi a, b lần lượt là phần thực và phần ảo của số phức
1
+
z
+
z...
Đọc tiếp
Cho số phức z thỏa mãn 5 z ¯ + i = 2 - i z + 1 . Gọi a, b lần lượt là phần thực và phần ảo của số phức 1 + z + z 2 , tổng a + b bằng
A. 13
B. -5
C. 9
D. 5
Cho số phức z thỏa mãn
2
+
i
z
+
2
1
+
2
i
1
+
i
7
+
8
i
. Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức
w...
Đọc tiếp
Cho số phức z thỏa mãn 2 + i z + 2 1 + 2 i 1 + i = 7 + 8 i . Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức w = z + 1 + i . Tính P = a 2 + b 2
A. P = 5
B. P = 7
C. P = 13
D. P = 25
Ta có
2
+
i
z
+
2
1
+
2
i
1
+
i
=
7
+
8
i
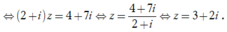
Suy ra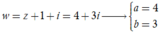 
Chọn D.
Đúng 0
Bình luận (0)
Nếu a ,b lần lượt là phần thực và phần ảo của số phức z1-i thì A. . B. . C. . D.
Đọc tiếp
Nếu a ,b lần lượt là phần thực và phần ảo của số phức z=1-i thì
A. 
.
B. 
.
C. 
.
D. 
Cho số phức z 2 + i. Phần ảo của số phức
z
z
+
1
z
-
1
là A. -2 B. -2i C. 2 D. 2i
Đọc tiếp
Cho số phức z = 2 + i. Phần ảo của số phức z = z + 1 z - 1 là
A. -2
B. -2i
C. 2
D. 2i
Gọi a và b lần lượt là phần thực và phần ảo của số phức
z
1
+
1
+
i
+
1
+
i
2
+
.
.
.
+
1
+
i...
Đọc tiếp
Gọi a và b lần lượt là phần thực và phần ảo của số phức z = 1 + 1 + i + 1 + i 2 + . . . + 1 + i 20 . Tính a +b.
A. 1 - 2 11
B. 1 - 2 20
C. 1.
D. 1 + 2 11
Phần thực và phần ảo của số phức z thỏa mãn: (1 + i)2(2 - i) z = 8 + i + (1 + 2i)z lần lượt là?
A. -3; -2
B. 2; 3
C. 2; -3
D. Đáp án khác.
Chọn C.
Ta có: ( 1 + i)2(2 - i) z = 8 + i + (1 + 2i)z
Nên z[( 1 + i)2(2 -i) – (1 + 2i) ] = 8 + i
Suy ra: z[2i(2 - i) – 1 - 2i] = 8 + i
Vậy số phức z đã cho có phần thực là 2, phần ảo là -3.
Đúng 0
Bình luận (0)
Cho số phức
z
(
1
-
i
)
(
a
+
b
i
)
1
+
i
thì phần ảo của z bằng: A. b B. -b C. a D. -a
Đọc tiếp
Cho số phức z = ( 1 - i ) ( a + b i ) 1 + i thì phần ảo của z bằng:
A. b
B. -b
C. a
D. -a
Gọi z là số phức có môđun nhỏ nhất và thỏa mãn
z
+
1
+
i
z
¯
+
i
. Tổng phần thực và phần ảo của số phức z bằng
Đọc tiếp
Gọi z là số phức có môđun nhỏ nhất và thỏa mãn z + 1 + i = z ¯ + i . Tổng phần thực và phần ảo của số phức z bằng
