Cho hàm sốy = f(x) có đạo hàm f ' x = x 2 x − 1 x − 4 2 . Khi đó số điểm cực trị của hàm số y = f x 2 là
A. 3
B. 4
C. 5
D. 2
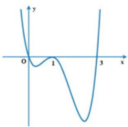
Cho hàm sốy=f(x) có đạo hàm f'(x) trên tập số thực ℝ và đồ thị của hàm số y=f(x) như hình vẽ. Khi đó, đồ thị của hàm số y = ( f ( x ) ) 2 có
A. 2 điểm cực đại, 2 điểm cực tiểu
B. 2 điểm cực tiểu, 3 điểm cực đại
C. 1 điểm cực đại, 3 điểm cực tiểu
D. 2 điểm cực đại, 3 điểm cực tiểu
Từ đồ thị hàm số f(x) ta thấy đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ x=0;x=1;x=3
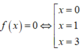
Lại thấy đồ thị hàm số y=f(x) có ba điểm cực trị nên
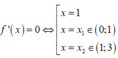
Hàm số y = f x 2 có đạo hàm y'=2f(x).f '(x)
Xét phương trình
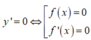
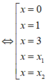
Ta có BXD của y' như sau
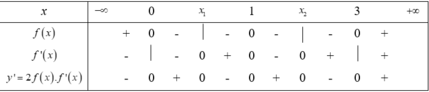
Nhận thấy hàm số y = f x 2 có y' đổi dấu từ âm sang dương tại ba điểm x=0;x=1;x=3 nên hàm số có ba điểm cực tiểu. Và y' đổi dấu từ dương sang âm tại hai điểm x = x 1 ; x = x 2 nên hàm số có hai điểm cực đại.
Chọn đáp án D.
Cho hàm sốy =f(x), y =g(x)liên tục trên ℝ và có đồ thị các đạo hàm (đồ thị y =g’(x) là đường đậm hơn) như hình vẽ
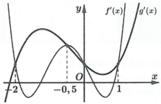
Hàm số h(x) =f(x-1) –g(x-1) nghịch biến trên khoảng nào dưới đây?
A. (1/2;1).
B. (-1;1/2).
C. (1;+∞).
D. (2;+∞)
Cho hàm sốy = f(x). Hàm số y = f’(x) có đồ thị như hình bên. Hàm số y = f(2-x) đồng biến trên khoảng
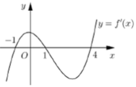
A. (1;3).
B. (2;+∞).
C. (-2;1).
D. (-∞;-2).
Cho hàm sốy=f(x). Hàm số y=f’(x) có đồ thị như hình bên. Tìm số điểm cực trị của hàm số y=f(x)

A. 0
B. 1
C. 2
D. 3
Đáp án B
Nhìn vào đồ thị hàm số ta thấy có một giá trị của x (gải sử x = a) để y’=0 và không có giá trị nào của x làm y’ không xác định. Mặt khác y' đổi dấu từ dương sang âm khi đi qua x = a do vậy x = a là một điểm cực trị của hàm số y=f(x).
Ta chọn B
Cho hàm sốy = f(x). Hàm số y = f’(x) có đồ thị như hình vẽ dưới đây.
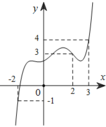
Đặt g x = 2 f x - x + 1 2 .Biết f(-2) = =f(3). Mệnh đề nào đúng?
A. m a x - 2 ; 3 g x = g 3 , m i n - 2 ; 3 g x = g - 2
B. m a x - 2 ; 3 g x = g 2 , m i n - 2 ; 3 g x = g 3
C. m a x - 2 ; 3 g x = g 2 , m i n - 2 ; 3 g x = g - 2
D. m a x - 2 ; 3 g x = g - 2 , m i n - 2 ; 3 g x = g 2
Cho hàm sốy=f(x) . Hàm số y=f'(x) có bảng biến thiên như hình vẽ sau: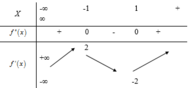
Tìm số điểm cực trị của hàm số: y=f(x).
![]()
![]()
![]()
![]()
Cho hàm sốy=f(x) . Hàm số y=f'(x)có bảng biến thiên như hình vẽ sau:
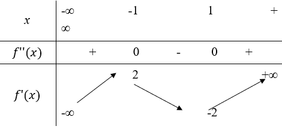
Tìm số điểm cực trị của hàm số: y=f(x).
A. 0.
B. 1
C. 2.
D. 3.
Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:
a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)
b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)
Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm số:
a) \(y=f(2-3x)\)
b) \(y=f(x^2+1)\)
c) \(y=f(3x+1)\)
Biết hàm số f ( x ) - f ( 2 x ) có đạo hàm bằng 5 tại x = 1 và đạo hàm bằng 7 tại x = 2 Tính đạo hàm của hàm số f ( x ) - f ( 4 x ) tại x = 1.
A. 8.
B. 12.
C. 16.
D. 19.