Giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = x = ln(x) trên đoạn 1 2 ; e lần lượt là
A. 1 và e - 1
B. 1 và e
C. 1 2 + ln 2 và e - 1
D. 1 và 1 2 + ln 2
Tìm giá trị lớn nhất và nhỏ nhất của hàm số f(x) = 2x2- ln( 3-4x) trên đoạn [ -2; 0]
A. Max y=8; min y=1-ln4
B. max y=8-ln11; miny=1/8 -ln4
C. max y=8+ln11; min y=-ln4
D. max y=8+ln 4; min y=4+ln11
tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số trên đoạn [2;4]
y=\(\dfrac{x^2+3}{x-1}\)
Giá trị nhỏ nhất của hàm số y = l n ( x 2 - 2 x + 1 ) - x trên đoạn [2;4] là:
A. 2ln2 - 3
B. 2ln2 - 4
C. - 2
D. - 3
Gọi M; N lần lượt là giá trị nhỏ nhất, lớn nhất của hàm số y = ln ( x + x 2 + 4 ) trên đoạn [0;5] Khi đó tổng M+N là
A. ![]()
B. 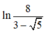
C. ![]() .
.
D. Kết quả khác
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = x 2 - 2 x + l n ( 2 x + 1 ) trên [0; 1]
A. m a x 0 ; 1 y = ln 3 + 1 ; m i n 0 ; 1 y = ln 2
B. m a x 0 ; 1 y = ln 3 - 1 ; m i n 0 ; 1 y = 0
C. m a x 0 ; 1 y = ln 3 - 1 ; m i n 0 ; 1 y = ln 2 - 3 4
D. m a x 0 ; 1 y = ln 2 + 3 4 ; m i n 0 ; 1 y = ln 3 - 1
Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau trên các khoảng, đoạn tương ứng: f(x) = x – ln x + 3 trên khoảng (0; ∞ )
min f(x) = f(1) = 4. Không có giá trị lớn nhất.
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = f(x) = x 2 − 4x + 3 trên đoạn [−2; 1].
A. M = 15; m = 1.
B. M = 15; m = 0.
C. M = 1; m = −2.
D. M = 0; m = −15.
Giá trị nhỏ nhất của hàm số f ( x ) = l n ( x 2 + x + 1 ) trên đoạn [-2;0] bằng
A. ln3.
B. 0.
C. -2 ln2.
D. ln3-2 ln2.
Tìm giá trị lớn nhất của hàm số f(x)=x(2-ln x) trên đoạn [2;3].
A.![]()
B. ![]()
C. ![]()
D. ![]()