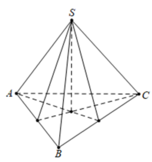
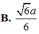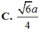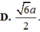Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a, góc tạo bởi hai mặt phẳng S A B và A B C bằng 60 ° . Diện tích xung quanh của hình nón đỉnh S và đường tròn đáy ngoại tiếp tam giác ABC bằng
A. 7 π a 2 3
B. 7 π a 2 6
C. 3 π a 2 3
D. 3 π a 2 6
Những câu hỏi liên quan
Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a, góc tạo bởi hai mặt phẳng (SAB) và (ABC) bằng
60
0
. Diện tích xung quanh của hình nón đỉnh S và đường tròn đáy ngoại tiếp tam giác ABC bằng
Đọc tiếp
Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a, góc tạo bởi hai mặt phẳng (SAB) và (ABC) bằng 60 0 . Diện tích xung quanh của hình nón đỉnh S và đường tròn đáy ngoại tiếp tam giác ABC bằng
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , cạnh bên SA vuông góc với đáy a. Biết góc tạo bởi hai mặt phẳng (SBC) và (ABC) bằng
60
0
, tính thể tích của khối chóp .
Đọc tiếp
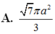
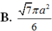
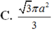
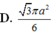
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , cạnh bên SA vuông góc với đáy a. Biết góc tạo bởi hai mặt phẳng (SBC) và (ABC) bằng 60 0 , tính thể tích của khối chóp .
Cho hình chóp S.ABC có ABC là tam giác đều cạnh a và SA vuông góc với đáy. Góc tạo bởi mặt phẳng (SBC) và mặt phẳng (ABC) bằng 30º. Khi đó thể tích của khối chóp S.ABC được tính theo a là: A.
a
3
12
.
B.
a
3
3
8
.
C.
a
3...
Đọc tiếp
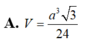
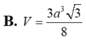
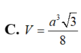
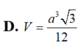
Cho hình chóp S.ABC có ABC là tam giác đều cạnh a và SA vuông góc với đáy. Góc tạo bởi mặt phẳng (SBC) và mặt phẳng (ABC) bằng 30º. Khi đó thể tích của khối chóp S.ABC được tính theo a là:
A. a 3 12 .
B. a 3 3 8 .
C. a 3 3 24 .
D. a 3 4 .
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , cạnh bên SA vuông góc với đáy(ABC) . Biết góc tạo bởi hai mặt phẳng ( SBC) và (ABC)bằng
60
°
, tính thể tích của khối chóp . A.
V
a
3
3
24
B.
V
3
a...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , cạnh bên SA vuông góc với đáy(ABC) . Biết góc tạo bởi hai mặt phẳng ( SBC) và (ABC)bằng 60 ° , tính thể tích của khối chóp .
A. V = a 3 3 24
B. V = 3 a 3 3 8
C. V = a 3 3 8
D. V = a 3 3 12
Đáp án C
Phương pháp:
- Xác định góc giữa hai mặt phẳng S.ABC bởi định nghĩa:
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng nằm trong hai mặt phẳng mà cùng vuông góc với giao tuyến.
- Tính thể tích khối chóp theo công thức
V = 1 3 S h
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có ABC là tam giác đều cạnh a. Hai mặt phẳng (SAC), (SAB) cùng vuông góc với đáy và góc tạo bởi SC và đáy bằng 600. Tính khoảng cách h từ A tới mặt phẳng (SBC) theo a
Đọc tiếp
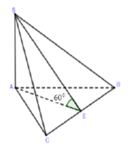
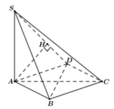
Cho hình chóp S.ABC có ABC là tam giác đều cạnh a. Hai mặt phẳng (SAC), (SAB) cùng vuông góc với đáy và góc tạo bởi SC và đáy bằng 600. Tính khoảng cách h từ A tới mặt phẳng (SBC) theo a
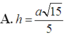
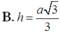
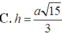
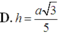
Đáp án A
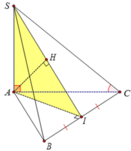
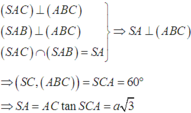
Gọi I,H lần lượt là hình chiếu vuông góc của A trên BC, SI, khi đó: d(A, (SBC)) =AH
Tam giác ABC đều cạnh a nên AI = a 3 2
Khi đó xét tam giác SAI :
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có ABC là tam giác đều cạnh a. Hai mặt phẳng (SAC), (SAB) cùng vuông góc với đáy và góc tạo bởi SC và đáy bằng
60
°
. Tính khoảng cách h từ A tới mặt phẳng (SBC) theo a. A.
h
a
15
5
B.
h
a
3
3
C.
h...
Đọc tiếp
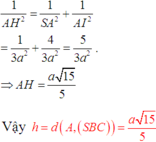
Cho hình chóp S.ABC có ABC là tam giác đều cạnh a. Hai mặt phẳng (SAC), (SAB) cùng vuông góc với đáy và góc tạo bởi SC và đáy bằng 60 ° . Tính khoảng cách h từ A tới mặt phẳng (SBC) theo a.
A. h = a 15 5
B. h = a 3 3
C. h = a 15 3
D. h = a 3 5
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và
A
B
a
. Cạnh bên SA vuông góc với mặt phẳng đáy , góc tạo bởi hai mặt phẳng (ABC) và (SBC) bằng
60
°
. Khoảng cách giữa hai đường thẳng AB và SC bằng A. a B.
a
2
2
C.
a
3
2
D....
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và A B = a . Cạnh bên SA vuông góc với mặt phẳng đáy , góc tạo bởi hai mặt phẳng (ABC) và (SBC) bằng 60 ° . Khoảng cách giữa hai đường thẳng AB và SC bằng
A. a
B. a 2 2
C. a 3 2
D. a 3 3
Xác định được 
Khi đó ta tính được 
Trong mặt phẳng (ABC) lấy điểm D sao cho ABCD là hình chữ nhật
=> AB//CD nên
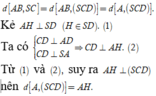
Xét tam giác vuông SAD có 
Chọn C.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB a, cạnh bên SA vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng (ABC) và (SBC) bằng
60
°
khi và chỉ khi SA bằng A.
3
a
B.
6
a
6
C.
6
a...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, cạnh bên SA vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng (ABC) và (SBC) bằng 60 ° khi và chỉ khi SA bằng
A. 3 a
B. 6 a 6
C. 6 a 4
D. 6 a 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB a, cạnh bên SA vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng (ABC) và (SBC) bằng 60
°
khi và chỉ khi SA bằng
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, cạnh bên SA vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng (ABC) và (SBC) bằng 60 ° khi và chỉ khi SA bằng
