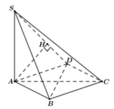
Xác định được ![]()
Khi đó ta tính được ![]()
Trong mặt phẳng (ABC) lấy điểm D sao cho ABCD là hình chữ nhật
=> AB//CD nên
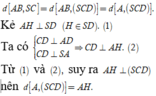
Xét tam giác vuông SAD có 
Chọn C.

Xác định được ![]()
Khi đó ta tính được ![]()
Trong mặt phẳng (ABC) lấy điểm D sao cho ABCD là hình chữ nhật
=> AB//CD nên
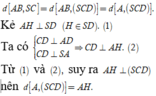
Xét tam giác vuông SAD có 
Chọn C.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, cạnh bên SA vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng (ABC) và (SBC) bằng 60 0 (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng AB và SC bằng :
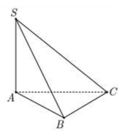
A. a
B. a 3 3
C. a 2 2
D. a 3 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, cạnh bên SA vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng (ABC) và (SBC) bằng 60 ° khi và chỉ khi SA bằng
A. 3 a
B. 6 a 6
C. 6 a 4
D. 6 a 2
Cho hình chóp S . A B C có đáy A B C là tam giác vuông cân tại A,AB=a cạnh bên SA vuông góc với đáy, góc tạo bởi giữa hai mặt phẳng S B C và A B C bằng 60 0 khi và chỉ khi SA bằng
A. 3 a .
B. 6 a 6 .
C. 6 a 4 .
D. 6 a 2 .
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mặt bên SBC là tam giác đều cạnh a và mặt phẳng (SBC) vuông góc với mặt đáy. Khoảng cách giữa hai đường thẳng SA và BC là
A. 2 a 2 .
B. a 2 .
C. 3 a 4 .
D. 3 a 2 .
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B ; A B = 3 a ; B C = 4 a . Cạnh bên SA vuông góc với mặt phẳng đáy. Góc tạo giữa SC và mặt phẳng đáy bằng 60 ° . Gọi M là trung điểm của AC. Khoảng cách giữa hai đường thẳng AB và SM bằng
A. a 3
B. 10 a 3 79
C. 5 a 3
D. 5 a 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mặt bên SBC là tam giác đều cạnh a và mặt phẳng (SBC) vuông góc với mặt đáy. Tính theo a khoảng cách giữa hai đường thẳng SA và BC.
A. a 22 11
B. a 4 3
C. a 11 22
D. a 3 4
Cho hình chóp S.ABC có ABC là tam giác đều cạnh a. Hai mặt phẳng (SAC), (SAB) cùng vuông góc với đáy và góc tạo bởi SC và đáy bằng 60 ° . Tính khoảng cách h từ A tới mặt phẳng (SBC) theo a.
A. h = a 15 5
B. h = a 3 3
C. h = a 15 3
D. h = a 3 5
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng 3. Gọi α là góc giữa hai mặt phẳng (SBC) và (ABC), tính cos α khi thể tích khối chóp S . A B C nhỏ nhất.
A. cos α = 2 2
B. cos α = 1 3
C. cos α = 3 3
D. cos α = 2 3
Cho hình chóp S.ABC có đáy là tam giác vuông cân cạnh bằng B, cạnh bên SA vuông góc với mặt phẳng đáy, AB=BC=a và SA=a. Góc giữa hai mặt phẳng (SAC) và (SBC) bằng
A. 90 0 .
B. 30 0 .
C. 60 0 .
D. 45 0 .