Cho lăng trụ ABC.A'B'C' có thể tích V. Tính thể tích của khối chóp A'.ABC theo V.
A. V 3
B. V 2
C. V 4
D. 2 3 V
Cho lăng trụ ABC.A'B'C' có thể tích V. Tính thể tích của khối chóp A'.ABC theo V.
A . V 3
B . V 2
C . V 4
D . 2 V 3
Cho lăng trụ tam giác ABC.A'B'C' có thể tích là V. Tính thể tích khối chóp A.BCC'B' theo V.
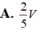
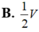
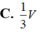
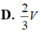
Cho khối lăng trụ ABC.A'B'C' có thể tích là V, thể tích của khối chóp C'.ABC là:
A. 2V
B. 1 2 V
C. 1 3 V
D. 1 6 V
Cho khối lăng trụ ABC.A'B'C' có thể tích là V. Điểm M là trung điểm của cạnh AA'. Tính theo V thể tích khối chóp M . B C C ' B '
A. 2V/3
B. 3V/4
C. V/3
D. V/2
Đáp án A
Ta có V A B C . A ' B ' C ' = V M . A B C + V M . A ' B ' C ' + V M . B C C ' B ' = 1 3 V A B C . A ' B ' C ' + V M . B C C ' B ' ⇒ V M . B C C ' B ' = 2 V 3
Tính thể tích V của khối chóp C'.ABC biết thể tích của khối lăng trụ ABC.A'B'C' bằng a3.
A. V=3a3
B. V=a3/3
C. V=a3/9
D. V=9a3.
Đáp án B
Gọi h là chiều cao lăng trụ.
Ta có:
V C ' . A B C = 1 3 . d C ' , A B C . S A B C = 1 3 . h . S A B C = 1 3 V L T = a 3 3
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A, B A C ^ = 120 o và BC =AA' = a 3 . Tính theo a thể tích V của khối lăng trụ ABC.A'B'C'.
A. V = 9 a 3 4
B. V = 3 3 a 3 6
C. V = 3 3 a 3 2
D. V = 3 a 3 4
1)Cho khối lập phương có độ dài đường chéo bằng \(\sqrt{3}\)cm. Tính thể tích khối lập phương đó
2) Cho hình khối lăng trụ tam giác ABC.A'B'C' có thể tích bằng 1. TÍnh thể tích khối chóp A'.ABC' theo V
3)Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tamiacs đều cạnh a và đường thẳng A'C tạo với mặt phẳng (ABB'A') một góc 300 . Tính thể tích khối lăng trụ ABC.A'B'C'
4)Cho hình chóp tam giác S.ABC có ASB=CSB=600 , SA=SB=SC=2a. Tính thể tích khối chóp S.ABCD
5) Cho hình chóp S.ABCD có SA vuông góc với (ABCD), SB=\(a\sqrt{5}\), ABCD là hình thoi cạnh a, góc ABC = 600 . Tính thể tích khối chóp S.ABCD
Cho hình lăng trụ A B C . A ' B ' C ' có thể tích bằng V . Gọi M là trung điểm cạnh B B ' , điểm N thuộc cạnh C C ' sao cho C N = 2 C ' N . Tính thể tích khối chóp A,BCNM theo V
A. V A . B C N M = 7 V 12
B. V A . B C N M = 7 V 18
C. V A . B C N M = V 3
D. V A . B C N M = 6 V 18
Chọn B.
Phương pháp:

+) So sánh diện tích hình thang BMNC và diện tích hình bình hành BCC’B’ từ đó suy ra tỉ số thể tích V A . B M N C V A . B C C ' B '
+) So sánh V A . B C C ' B ' với V.
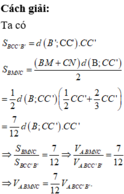
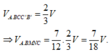
Cho lăng trụ A B C . A ' B ' C ' có thể tích V, gọi M, N lần lượt là trung điểm các cạnh BB', CC'. Tính thể tích khối chóp A . B C M N theo V.
A. V 2
B. V 3
C. 2 V 3
D. V 6