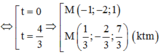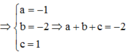Cho điểm A nằm trên mặt cầu (S). Qua A kẻ được bao nhiêu tiếp tuyến với mặt cầu (S) ?
A. 0
B. Vô số
C. 1
D. 2
Những câu hỏi liên quan
Từ điểm M nằm ngoài mặt cầu S(O;R) có thể kẻ được bao nhiêu tiếp tuyến với mặt cầu?
A. 0 B. 1
C. 2 D. Vô số
Chọn D.
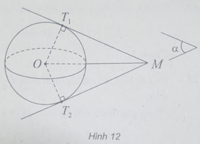
(h.12) Gọi ( α ) là mặt phẳng chứa đường thẳng MO
Ta có: ( α ) cắt mặt cầu S(O;R) theo giao tuyến là đường tròn (C) có tâm O, bán kính R.
Trong mặt phẳng ( α ), từ điểm M nằm ngoài (C) ta luôn kẻ được hai tiếp tuyến M T 1 , M T 2 với đường tròn (C). Đây cũng là hai tiếp tuyến với mặt cầu S(O;R).
Nhận xét: Do có vô số mặt phẳng ( α ) chứa đường thẳng MO. Những mặt phẳng này cắt mặt cầu S(O;R) theo các giao tuyến là đường tròn khác nhau nên cũng có vô số tiếp tuyến với mặt cầu được kẻ từ điểm M nằm ngoài mặt cầu.
Đúng 0
Bình luận (0)
Cho điểm A nằm trên mặt cầu S . Qua A kẻ được bao nhiêu tiếp tuyến với mặt cầu S ?
A. 0
B. Vô số
C. 1
D. 2
Đáp án B
Qua A kẻ được vô số tiếp tuyến với mặt cầu (S)
Đúng 0
Bình luận (0)
Cho điểm A nằm trên mặt cầu (S). Qua A kẻ được bao nhiêu tiếp tuyến với mặt cầu (S) ?
A. 0
B. Vô số
C. 1
D. 2
Cho điểm A nằm trên mặt cầu (S) Qua A kẻ được bao nhiêu tiếp tuyến với mặt cầu (S)?
A.0
B. Vô số
C.1
D. 2
Đáp án B
Qua A kẻ được vô số tiếp tuyến với mặt cầu (S)
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
x
-
4
y
+
6
z
-
13
0
và đường thẳng
d
:
x
+
1
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 - 2 x - 4 y + 6 z - 13 = 0 và đường thẳng d : x + 1 1 = y + 2 1 = z - 1 1 . Điểm M a ; b ; c a > 0 nằm trên đường thẳng d sao cho từ M kẻ được ba tiếp tuyến MA, MB, MC đến mặt cầu (S) (A, B, C là các tiếp điểm) và A M B ^ = 60 ° , B M C ^ = 90 ° , C M A ^ = 120 ° . Tính a 3 + b 3 + c 3
A. a 3 + b 3 + c 3 = 112 9
B. a 3 + b 3 + c 3 = 173 9
C. a 3 + b 3 + c 3 = - 8
D. a 3 + b 3 + c 3 = 23 9
Chọn đáp án A
Gọi O là tâm mặt cầu. Đặt MA = x
Do A, B, C là các tiếp điểm kẻ từ M đến mặt cầu nên ta có MA = MB = MC = x
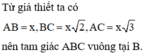
Gọi H là trung điểm AC, K là trung điểm AB. Ta có
Áp dụng hệ thức lượng trong tam giác OMC ta có
Đúng 0
Bình luận (0)
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
9
và điểm A(1;2;3). Từ A kẻ được ba tiếp tuyến AB,AC,AD đến mặt cầu (S) với A,B,C là các tiếp điểm. Hỏi mặt phẳng (BCD) đi qua điểm nào dưới đây ? A. M(1;1;1). B. N(1;1;2). C. P(0;1;1). D. Q(2;0;1).
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 = 9 và điểm A(1;2;3). Từ A kẻ được ba tiếp tuyến AB,AC,AD đến mặt cầu (S) với A,B,C là các tiếp điểm. Hỏi mặt phẳng (BCD) đi qua điểm nào dưới đây ?
A. M(1;1;1).
B. N(1;1;2).
C. P(0;1;1).
D. Q(2;0;1).
Trong không gian Oxyz, cho mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
x
-
4
y
+
6
z
-
13
0
và đường thẳng
d
:
x
+
1
1...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 - 2 x - 4 y + 6 z - 13 = 0 và đường thẳng d : x + 1 1 = y + 2 1 = z - 1 1 . Điểm M(a;b;c)(với a < 0) trên đường thẳng d sao cho từ M kẻ được ba tiếp tuyến MA, MB, MC đến mặt cầu (S) ( A, B, C là các tiếp điểm) thõa mãn các góc A M B ^ = 60 ° , B M C ^ = 90 ° , C M A ^ = 120 ° . Tính abc bằng
A. 4
B. 10 3
C. -2
D. 2
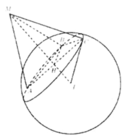
Tam giác ABC nội tiếp đường tròn nhỏ tâm H đường kính AC
Đúng 0
Bình luận (0)
Trong không gian Oxyz cho mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
x
-
4
y
+
6
z
-
13
0
và đường thẳng
d
:
x
+
1
1...
Đọc tiếp
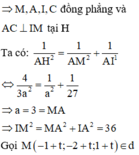
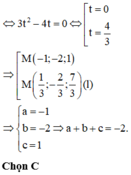
Trong không gian Oxyz cho mặt cầu
S : x 2 + y 2 + z 2 - 2 x - 4 y + 6 z - 13 = 0 và đường thẳng d : x + 1 1 = y + 2 1 = z - 1 1 . Tọa độ điểm M trên đường thẳng d sao cho từ M kẻ được 3 tiếp tuyến MA, MB, MC đến mặt cầu (S) (A, B, C là các tiếp điểm) thỏa mãn A M B ⏜ = 60 ° , B M C ⏜ = 90 ° , C M A ⏜ = 120 ° có dạng M (a;b;c) với a <0. Tổng a+b+c bằng:
A. 10 3 .
B. 2
C. - 2
D. 1
Trong không gian Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
-
2
x
-
4
y
+
6
z
-
13...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 2 x - 4 y + 6 z - 13 = 0 và đường thẳng d: x + 1 1 = y + 2 1 = z - 1 1 . Tọa độ điểm M trên đường thẳng d sao cho từ M kẻ được 3 tiếp tuyến MA, MB, MC đến mặt cầu (S) (A, B, C là các tiếp điểm) thỏa mãn A M B ^ = 60 0 ; B M C ^ = 90 0 ; C M A ^ = 120 0 có dạng M(a;b;c) với a<0 Tổng a + b + c bằng:
A. 2
B. - 2
C. 1
D. 10 3
Đáp án B.
Phương pháp: Tính độ dài đoạn thẳng IM với I là tâm mặt cầu.
Tham số hóa tọa độ điểm M, sau đó dựa vào độ dài IM để tìm điểm M.
Cách giải : Mặt cầu (S) có tâm I(1;2; – 3) bán kính R = 3 3
Đặt MA = MB = MC = a
Tam giác MAB đều => AB = a
Tam giác MBC vuông tại M => BC = a 2
Tam giác MCA có C M A ^ = 120 0 => AC = a 3
Xét tam giác ABC có A B 2 + B C 2 = A C 2 => ∆ABC vuông tại B
=>∆ABC ngoại tiếp đường tròn nhỏ có đường kính AC
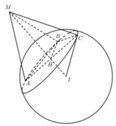
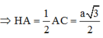
Xét tam giác vuông IAM có:
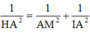
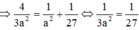
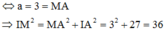
Đúng 0
Bình luận (0)