Các câu hỏi tương tự
Từ điểm M nằm ngoài mặt cầu S(O;R) có thể kẻ được bao nhiêu tiếp tuyến với mặt cầu?
A. 0 B. 1
C. 2 D. Vô số
Trong không gian Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
-
2
x
-
4
y
+
6
z
-
13
0
và đường thẳng ...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 2 x - 4 y + 6 z - 13 = 0 và đường thẳng d : x + 1 1 = y + 2 1 = z - 1 1 . Tọa độ điểm M trên đường thẳng d sao cho từ M kẻ được 3 tiếp tuyến MA, MB, MC đến mặt cầu (S) (A, B, C là các tiếp điểm) thỏa mãn A M B ^ = 60 o , B M C ^ = 90 o , C M A ^ = 120 o có dạng M(a;b;c) với a<0. Tổng a+b+c bằng:
A. 2
B. -2
C. 1
D. 10 3
Trong không gian Oxyz cho mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
2
x
-
4
y
+
6
z
-
13
0
và đường thẳng
d
:
x
+
1
1...
Đọc tiếp
Trong không gian Oxyz cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x - 4 y + 6 z - 13 = 0 và đường thẳng d : x + 1 1 = y + 2 1 = z - 1 1 . Tọa độ điểm M trên đường thẳng d sao cho từ M kẻ được 3 tiếp tuyến MA, MB, MC đến mặt cầu (S) (A, B, C là các tiếp điểm) thỏa mãn A M B ⏜ = 60 0 , B M C ⏜ = 90 0 , C M A ⏜ = 120 0 có dạng M(a;b;c) với a<0. Tổng a+b+c bằng:
A. 10 3 .
B. 2.
C. -2.
D. 1.
Trong không gian Oxyz, cho mặt cầu
S
:
x
2
+
y
2
+
x
+
2
2
16
và điểm A(m;m;2) nằm ngoài mặt cầu. Từ A kẻ các tiếp tuyến đến mặt cầu (S), gọi
P
m
là mặt phẳng chứa các tiếp điểm, biết ...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu S : x 2 + y 2 + x + 2 2 = 16 và điểm A(m;m;2) nằm ngoài mặt cầu. Từ A kẻ các tiếp tuyến đến mặt cầu (S), gọi P m là mặt phẳng chứa các tiếp điểm, biết P m luôn đi qua một đường thẳng d cố định, phương trình đường thẳng d là:
A. 
B. 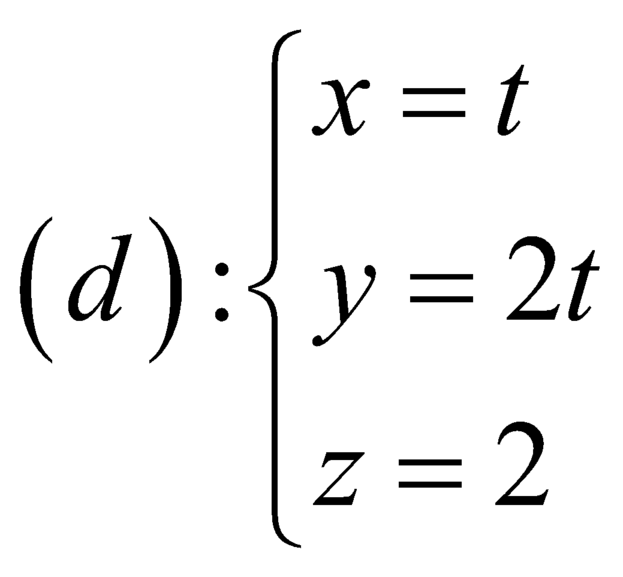
C. 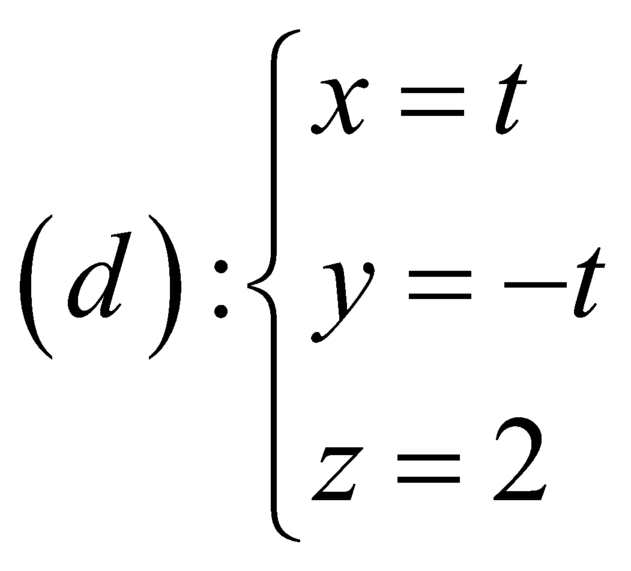
D. 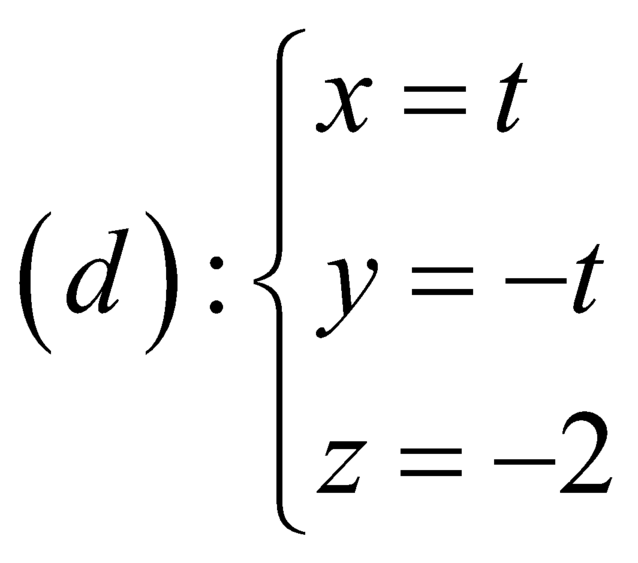 .
.
Cho đường tròn (C) và điểm A nằm ngoài mặt phẳng chứa (C). Có tất cả bao nhiêu mặt cầu chứa đường tròn (C) và đi qua A?
A. 0 B. 1
C. 2 D. Vô số
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
-
1
1
y
+
2
1
z
1
và mặt phẳng (P): 2x+y-2z+20. Gọi (S) là mặt cầu có tâm nằm trên d, tiếp xúc với mặt phẳng (P) và đi qua điểm A(2;-1;0). Biết tâm của mặt cầu có cao độ không nhỏ hơn 1,...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 1 1 = y + 2 1 = z 1 và mặt phẳng (P): 2x+y-2z+2=0. Gọi (S) là mặt cầu có tâm nằm trên d, tiếp xúc với mặt phẳng (P) và đi qua điểm A(2;-1;0). Biết tâm của mặt cầu có cao độ không nhỏ hơn 1, phương trình mặt cầu (S) là:
![]()
![]()
![]()
![]()
Cho hai điểm A(1;0;0), B(2;0;-1) và mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
x
-
2
+
1
0
. Có tất cả bao nhiêu mặt phẳng chứa hai điểm A, B và tiếp xúc với mặt cầu (S)?
Đọc tiếp
Cho hai điểm A(1;0;0), B(2;0;-1) và mặt cầu S : x 2 + y 2 + z 2 - 2 x - 2 + 1 = 0 . Có tất cả bao nhiêu mặt phẳng chứa hai điểm A, B và tiếp xúc với mặt cầu (S)?
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt cầu (S): \(x^2 + y^2 + (z+\sqrt(2))^2 = 3\)
Có tất cả bao nhiêu điểm A(a; b; c) (a, b, c là các số nguyên) thuộc mặt phẳng (Oxy) sao cho có ít nhất hai tiếp tuyến của (S) đi qua A và hai tiếp tuyến đó vuông góc với nhau?
Trong không gian Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
(
z
-
1
)
2
4
và điểm A(2;2;1). Từ điểm A kẻ ba tiếp tuyến AB, AC, AD với B, C, D là các tiếp điểm. Viết phương trình mặt phẳng (BCD).
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + ( z - 1 ) 2 = 4 và điểm A(2;2;1). Từ điểm A kẻ ba tiếp tuyến AB, AC, AD với B, C, D là các tiếp điểm. Viết phương trình mặt phẳng (BCD).
![]()
![]()
![]()
![]()




