Cho phương trình tanx+tan x + π 4 = 1. Diện tích của đa giác tạo bởi các điểm trên đường tròn lượng giác biểu diễn các họ nghiệm của phương trình gần với số nào nhất trong các số dưới đây?
A. 0,948
B. 0,949
C. 0,946
D. 0,947
Giải phương trình sau: tanx + tan (x+π/4) = 1
Điều kiện:
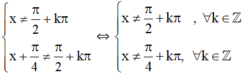
⇔ tan x.(1 - tanx) + tanx + 1 = 1 – tan x.
⇔ tan x - tan2x + 2.tan x = 0
⇔ tan2x - 3tanx = 0
⇔ tanx(tanx - 3) = 0
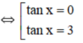
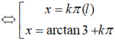
Vậy phương trình đã cho có tập nghiệm là:
{arctan 3+kπ; k ∈ Z }
Cho phương trình tan x + tan x + π 4 = 1 . Diện tích của đa giác tạo bởi các điểm trên đường trọn lương giác biểu diễn các họ nghiệm của phương trình gần với số nào nhất trong các số dưới đây?
A. 0,946.
B. 0,947.
C. 0,948.
D. 0,949.
Cho phương trình tan x + tan x + π 4 = 1 . Diện tích của đa giác tạo bởi các điểm trên đường trọn lương giác biểu diễn các họ nghiệm của phương trình gần với số nào nhất trong các số dưới đây?
A. 0,946
B. 0,947.
C. 0,948
D. 0,949
Đáp án D
Điều kiện cos x ≠ 0 cos x + π 4 ≠ 0
tan x + tan x + π 4 = 1 ⇔ tan x + tan x + 1 1 − tan x − 1 = 0
⇔ − tan 3 x + 3 tan x 1 − tan x = 0 ⇔ tan x ≠ 1 tan x 3 − tan x = 0 ⇔ tan x = 0 tan x = 3
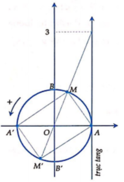
Ta có biểu thị các họ nghiệm của phương trình trẻn đường trọn lượn giác như hình bên.
Vậy đa giác tạo bởi các điểm trên đường tròn lượng giác biểu diễn các họ nghiệm của phương trình tan x + tan x + π 4 = 1 là tứ giác A M A ' M ' .
Cách 1: Đường thẳng có phương trình y = 3 x ⇔ 3 x − y = 0 .Khoảng cách từ điểm A 1 ; 0 đến M M ' là 3.1 − 0 3 2 + 1 2 = 3 10 . Do đó diện tích tứ giác A M A ' M ' là
S A M A ' M ' = 2 S A M M ' = 2. 1 2 . M M ' . d A , M M ' = 2. 3 10 ≈ 2.0,949
Cách 2: Ta có sin M O A ^ = 3 3 2 + 1 2 = 3 10
⇒ S A M A ' M ' = 4. S M O A = 4. 1 2 . O M . O A . sin M O A ^ = 2. 3 10 ≈ 2.0,949
Ta chọn D, do chỉ có 0,949 gần 2.0,949 nhất.
Cho phương trình tan x + tan x + π 4 = 1. Diện tích của đa giác tạo bởi các điểm trên đường tròn lượng giác biểu diễn các họ nghiệm của phương trình gần với số nào nhất trong các số dưới đây?
A. 0,948
B. 0,949
C. 0,946
D. 0,947
Đáp án B
Điều kiện: cos x ≠ 0 tan x ≠ 1
Ta có:
tan x + tan x + π 4 = 1 ⇔ tan x + tan x + tan π 4 1 − tan x . tan π 4 = 1
⇔ tan x + tan x + 1 1 − tan x = 1 ⇔ tan x − tan 2 x + tan x + 1 = 1 ⇔ tan x = 0 tan x = 2 ⇔ x = k π x = arctan 2 + k π k ∈ ℤ
suy ra 4 nghiệm trên đường tròn lượng giác là x = 0 x = π và x = arctan 2 x = arctan 2 + π
Vậy diện tích cần tính là S = 0 , 948
Cho phương trình tan x + tan x + π 4 = 1 Diện tích của đa giác tạo bởi các điểm trên đường tròn lượng giác biểu diễn các họ nghiệm của phương trình gần với số nào nhất trong các số dưới đây?
A. 0,948
B. 0,949
C. 0,946
D. 0,947
Diện tích của hình phẳng được giới hạn bởi các đường: y = tanx; y = 0; x = -π/4 và x = π/4 bằng:
A. π; B. -π;
C. ln2; D. 0
Đáp án: C.
Hướng dẫn: Diện tích được tính bởi tích phân
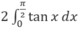
Diện tích của hình phẳng được giới hạn bởi các đường: y = tanx; y = 0; x = - π /4 và x = π /4 bằng:
A. π ; B. - π ;
C. ln2; D. 0
Đáp án: C.
Hướng dẫn: Diện tích được tính bởi tích phân
![]()
Họ nghiệm của phương trình tan(x+\(\frac{\pi}{5}\))+ \(\sqrt{3}\)= 0 là?
Phương trình tanx= tanx/2 có họ nghiệm là?
Nghiệm của phương trình √3 + 3tanx =0 có nghiệm là?
Phương trình √3 + tanx = 0 có nghiệm là?
Họ nghiệm của phương trình tan2x - tanx = 0 là?
Phương trình lượng giác 3cotx - √3 = 0 có nghiệm là?
Pt lượng giác 2cotx - √3 = 0 có nghiệm là?
Số nghiệm thuộc khoảng 0 ; π của phương trình tan x + sin x + tan x − sin x = 3 tan x là.
A. 0
B. 1.
C. 2
D. 3
Đáp án B
TABLE f ( x ) = tan x + sin x + tan x − sin x − 3 tan x đổi dấu 1 lần trong 0 ; π ⇒ 1 nghiệm