Đáp án A.

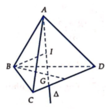
Gọi I là tâm mặt cầu ngoại tiếp ABCD ⇒ I ∈ Δ  và I A = I B = R  

 Thể tích mặt cầu ngoại tiếp ABCD nhỏ nhất <=> IB nhỏ nhất

⇔ I B ⊥ Δ ⇔ I ≡ G ⇒ I A = I B = B G = a 3 3 = A G ⇒ V A B C D = 1 3 S B C D . A G = 1 3 . 1 2 . a . a 3 2 . a 3 3 = a 2 12

zồi ôi dài quá

Sửa đề: CHo ΔABC vuông tại A có \(\hat{ABC}=60^0\)

a: ΔABC vuông tại A

=>\(\hat{ABC}+\hat{ACB}=90^0\)

=>\(\hat{ACB}=90^0-60^0=30^0\)

Xét ΔABC có \(\hat{ABC}>\hat{ACB}\left(60^0>30^0\right)\)

mà AC,AB lần lượt là cạnh đối diện của các góc ABC, ACB

nên AC>AB

Xét ΔABC có AB<AC

mà HB,HC lần lượt là hình chiếu của AB,AC trên BC

nên HB<HC

b: Xét ΔAHB vuông tại H và ΔAHM vuông tại H có

AH chung

HB=HM

Do đó: ΔAHB=ΔAHM

=>AB=AM

Xét ΔABM có AB=AM và \(\hat{ABM}=60^0\)

nên ΔABM đều

c: Ta có: ΔMAB đều

=>\(\hat{MAB}=\hat{MBA}=60^0\)

Ta có: \(\hat{MAB}+\hat{MAC}=\hat{BAC}=90^0\)

\(\hat{MBA}+\hat{MCA}=90^0\) (ΔABC vuông tại A)

mà \(\hat{MAB}=\hat{MBA}\)

nên \(\hat{MAC}=\hat{MCA}\)

=>MA=MC

mà MA=MB

nên MB=MC

=>M là trung điểm của BC

ΔMAB đều

=>AB=BM

mà BC=2BM

nên BC=2BA
=>BC=8(cm) và AM=4cm

Xét ΔABC có

AM,BN là các đường trung tuyến

AM cắt BN tại O

Do đó: O là trọng tâm của ΔABC

=>\(AO=\frac23AM=\frac23\cdot4=\frac83\left(\operatorname{cm}\right)\)

Đáp án: C

Thay lần lượt tọa độ của ba điểm A, B, C vào đường thẳng Δ ta được:

A: 1 - 2.0 + 1 = 2 > 0

B: 2 - 2.(-3) + 1 = 9 > 0

C: -2 - 2.4 + 1 = -9 < 0

Ta thấy: A và C nằm khác phía so với Δ nên Δ cắt cạnh AC

B và C nằm khác phía so với Δ nên Δ cắt cạnh BC