Đáp án C

Ta có  f x = 2 x + m − 1 x + 1 → f ' x = 3 − m x + 1 2 ; ∀ x ∈ 1 ; 2

TH1: Với m < 3 ,  suy ra f ' x > 0 ; ∀ ∈ 1 ; 2 ⇒ f 2 = 1 ⇔ 3 + m 3 = 1 ⇔ m = 0  (nhận)

TH2: Với m>3 suy ra f ' x < 0 ; ∀ ∈ 1 ; 2 ⇒ f 1 = 1 ⇔ 1 + m 2 = 1 ⇔ m = 1  (loại)

Vậy m = 0  là giá trị cần tìm

x - y = m                           ( 1 ) x 2 - x y - m - 2 = 0   ( 2 )

Từ (1), ta có y = x - m , thế vào (2) ta được phương trình:

 x² – x (x- m) – m - 2= 0 ⇔ x² – x² + mx –m –2 = 0

hay mx –m -2 = 0 (*) .

Hệ phương trình đã cho có nghiệm khi phương trình (*) có nghiệm ⇔ m ≠ 0 .

Chọn B.

Đáp án B

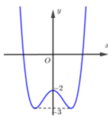
Dựa vào đồ thị hàm số  y = x 4 − 2 x 2 − 2

Suy ra − 3 < m < − 2  là giá trị cần tì

x^3-x^2(m+3)+x(3m+2)-2m=0

=>(x-1)(x^2-(m+2)x+2m)=0

=>x=1 hoặc x^2-(m+2)x+2m=0

Để PT có 3 nghiệm thì (m+2)^2-4*2m>0 và 1^2-(m+2)+2m<>0

=>m<>1 và m<>2

=>x2=(m+2-m+2)/2=2 và x3=(m+2+m-2)/2=m

Để tạo thành cấp sô nhân thì

x1<x2<m hoặc  m<x1<x2  hoặc x1<m<x2

=>m*1=2^2 hoặc 2m=1 hoặc m^2=2

=>m=4 hoặc m=1/2 hoặc m=căn 2

* Nếu m= 0 thì bất phương trình đã cho trở  thành: 

0x < 0(  luôn đúng với mọi x).

* Nếu  m= 1 thì bất phương trình đã cho  trở thành:

0x < 1 ( luôn đúng với mọi x)

Tập tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x là {0; 1}

Để xét bất phương trình bậc nhất vô nghiệm hay luôn đúng với mọi x ta chỉ cần xét hệ số a= 0.

* Với m = 0 thì bất phương  trình đã cho trở thành:

        0 x ≤ 0 ( luôn đúng với mọi  x)   ( loại)

* Với m = -3 thì bất phương trình đã cho trở thành:

        0 x ≤ 9   (luôn đúng với mọi  x)   ( loại)

Vậy không có giá trị nào của m để bất phương trình đã cho vô nghiệm

Chọn D