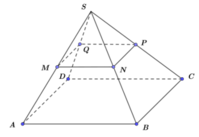
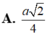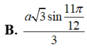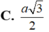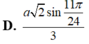Cho hình chóp tứ giác S.ABCD có M,N,P,Q lần lượt là trung điểm của các cạnh . Tỉ số V S . M N P Q V S . A B C D là
A. 1 18
B. 1 16
C. 3 8
D. 1 6
Cho hình chóp tứ giác S.ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh SA, SB, SC, SD. Tỉ số là V S . M N P Q V S . A B C D là:
A. 1 8
B. 1 16
C. 3 8
D. 1 6
Đáp án A
Theo công thức tỉ lệ tứ diện, ta có:

Theo dãy tỉ số bằng nhau ta có


Cho hình chóp tứ giác S.ABCD có M, N,P,Q lần lượt là trung điểm các cạnh SA, SB,SC,SD Biết khối chóp S.ABCD có thể tích bằng 16 a 3 Tính thể tích khối chóp S.MNPQ theo a
A. 2 a 3
B. a 3
C.8 a 3
D.4 a 3
Cho hình chóp tứ giác S.ABCD có M, N, P, Q lần lượt là trung điểm các cạnh SA, SB, SC, SD. Biết khối chóp S.ABCD có thể tích bằng 16 a 3 . Tính thể tích khối chóp S.MNPQ theo a
A. 2 a 3
B. a 3
C. 8 a 3
D. 4 a 3
Đáp án A
(với h’ và h lần lượt là khoảng cách từ S đến (MNPQ) và (ABCD)).
![]()
=> Chọn phương án A.
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi S là tâm A'B'C'D'. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Chứng minh S.MNPQ là hình chóp tứ giác đều.
b) Gọi thể tích hình chóp S.MNPQ là V' và thể tích hình lập phương là V. Tính tỉ số V'/V
Tương tự 2A.
a) Hình chóp S.MNPQ là hình chóp đều vì các mặt bên là tam giác cân và đáy MNPQ là đa giác đều.
b)
V
'
V
=
1
6
. Chú ý 
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh bên SA, SB, SC, SD (H.4.27). Chứng minh rằng tứ giác MNPQ là hình bình hành,
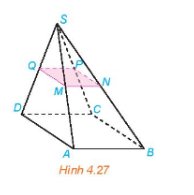
Xét tam giác SAB ta có: MN là đường trung bình suy ra MN // AB.
Tương tự ta có: NP // BC, PQ // CD, MQ // AD.
Mà ABCD là hình bình hành nên AB // CD, AD// CD, suy ra MN // PQ, MQ // NP.
Như vậy, MNPQ là hình bình hành.
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng (P) qua AK cắt các cạnh SB, SD lần lượt tại M, N. Gọi V và V’ lần lượt là thể tích các khối chóp S.ABCD và S.AMKN. Tỉ số V ' V có giá trị nhỏ nhất bằng
A. 1 5 .
B. 3 8 .
C. 1 3 .
D. 1 2 .
Đáp án C
Giả sử S D → = m . S M → ; S B → = n . S N → .
S A → + S C → = S B → + S D →
Do A; M; N; K đồng phẳng nên m + n = 3 .
V S . A K M V S . A B C = 1 2 .1. 1 m = 1 2 m ⇒ V S . A K M V = 1 4 m
Tương tự ta có V S . A K N V = 1 4 n ⇒ V ' V = 1 4 . m + n m n = 3 4 m n ≥ 3 m + n 2 = 3 3 2 = 1 3 .
Dấu bằng xảy ra khi m = n = 1,5 .
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi K là trung điểm SC. Mặt phẳng (P) qua AK cắt các cạnh SB, SD lần lượt tại M, N. Gọi V và V’ lần lượt là thể tích các khối chóp S.ABCD và S.AMKN. Tỉ số V ' V có giá trị nhỏ nhất bằng
A. 1 5
B. 3 8
C. 1 3
D. 1 2
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M, N lần lượt là trung điểm của các cạnh SA, SB. Chứng minh rằng tứ giác MNCD là hình thang.
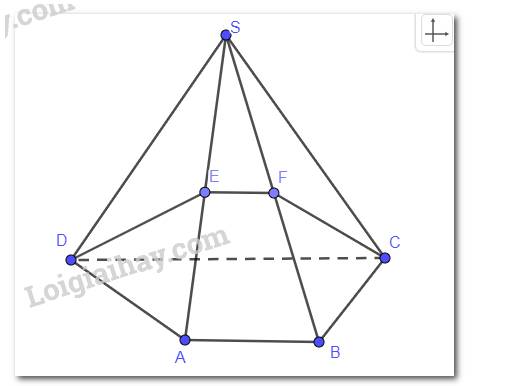
Xét tam giác SAB ta có MN là đường trung bình suy ra MN // AB.
Mà AB // CD do đó MN // CD.
Suy ra MNCD là hình thang.
Cho hình chóp tứ giác đều S.ABCD có SA=a và SAB= 11 π 24 . Gọi Q là trung điểm cạnh SA. Trên các cạnh SB,SC,SD lần lượt lấy các điểm M,N,P không trùng với các đỉnh hình chóp. Tìm giá trị nhỏ nhất của tổng AM+MN+NP+PQ theo a