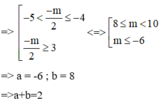Biết rằng a, b là hai giá trị thực để hàm số f x = x + 2 − a x x − 2 , x > 2 a x + b , x ≤ 2 liên tục tại x = 2 . Tính giá trị biểu thức P = a + 4 b
A. -10
B. 6
C. 2
D. -6
Cho hàm số f(x)= 2 x 3 + a x 2 - 4 x + b ( x - 1 ) 2 k h i x ≠ 1 3 c + 1 k h i x = 1 . Biết rằng a, b, c là giá trị thực để hàm số liên tục tại x 0 = 1 . Giá trị c thuộc khoảng nào sau đây?
A. c ∈ ( 0 ; 1 )
B. c ∈ 1 ; 2
C. c ∈ 2 ; 3
D. c ∈ 3 ; 4
Cho hàm số y=f(x) là hàm đa thức với hệ số thực. Hình vẽ bên dưới là một phần đồ thị của hai hàm số: y=f(x) và y=f'(x)
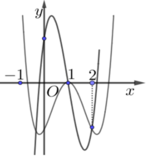
Tập các giá trị của tham số m để phương trình f ( x ) = m e x có hai nghiệm phân biệt trên [0;2] là nửa khoảng [a;b). Tổng a+b gần nhất với giá trị nào sau đây?
A. -0.81
B. -0.54
C. -0.27
D. 0.27
Cho hàm số f ( x ) = | 8 x 4 + a x 2 + b | , trong đó a, b là tham số thực. Biết rằng giá trị lớn nhất của hàm số f(x) trên đoạn [-1;1] bằng 1. Hãy chọn khẳng định đúng?
A. ![]() ,
, ![]()
B. ![]() ,
, ![]()
C. ![]() ,
, ![]()
D. ![]() ,
, ![]()
Đáp án C
Đặt ![]() khi đó ta có
khi đó ta có ![]() .
.
Vì ![]() nên
nên ![]() .
.
Theo yêu cầu bài toán thì ta có: ![]() với mọi
với mọi ![]() và có dấu bằng xảy ra.
và có dấu bằng xảy ra.
Đồ thị hàm số ![]() là một parabol có bề lõm quay lên trên do đó điều kiện trên dẫn đến hệ điều kiện sau xảy ra :
là một parabol có bề lõm quay lên trên do đó điều kiện trên dẫn đến hệ điều kiện sau xảy ra :

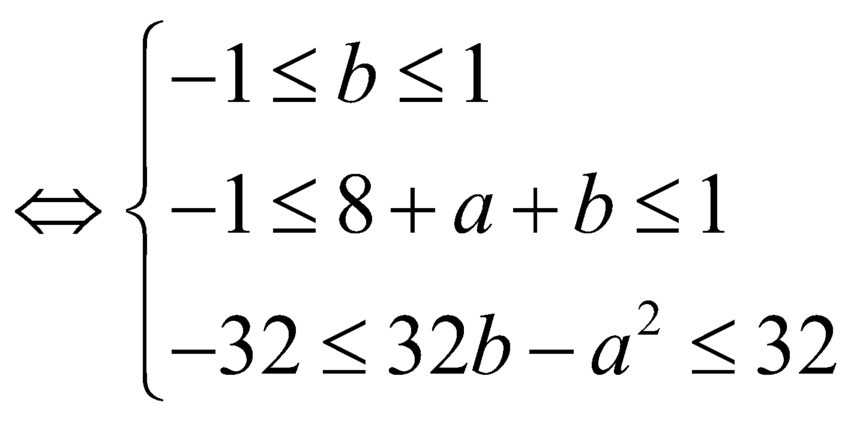
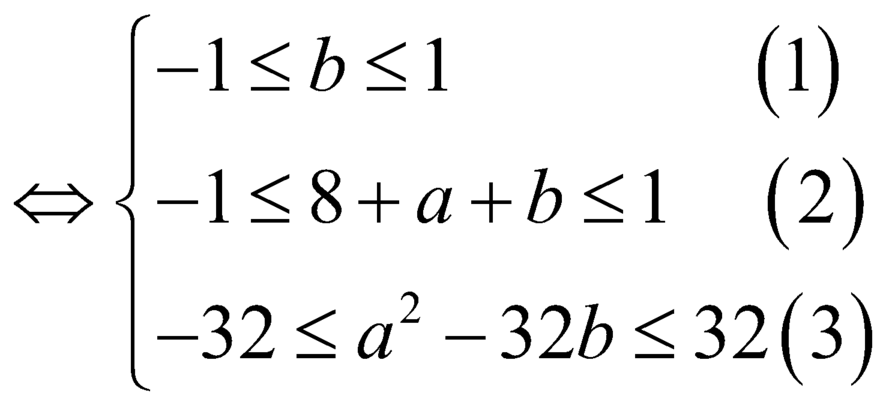
Lấy ![]() ta có :
ta có : ![]() do đó
do đó ![]() .
.
Lấy ![]() ta có :
ta có : ![]()
Suy ra : ![]()
![]() .
.
Khi đó ta có ![]() và
và ![]() .
.
Kiểm tra : ![]()
![]()
Vì ![]() nên
nên ![]()
![]()
![]() .
.
Vậy ![]() khi
khi ![]() (t/m).
(t/m).
Cho hai hàm đa thức y = f(x), y = g(x) có đồ thị là hai đường cong ở hình vẽ. Biết rằng đồ thị hàm số y = f(x) có đúng một điểm cực trị là A, đồ thị hàm số y = g(x) có đúng một điểm cực trị là B và A B = 7 4 . Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-5;5) để hàm số y = f ( x ) - g ( x ) + m có đúng 5 điểm cực trị?
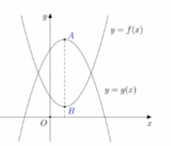
A. 1
B. 3
C. 4
D. 6
Cho hàm số y=f(x) là hàm đa thức hệ số thực. Hình vẽ bên là đồ thị của hai hàm số y=f(x) và y=f'(x) . Phương trình f(x)= m e x có hai nghiệm thực phân biệt thuộc đoạn [0;2] khi và chỉ khi m thuộc nửa khoảng [a;b). Giá trị của a+b gần nhất với giá trị nào dưới đây ?
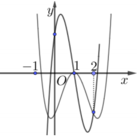
A. 0,27.
B. −0,54.
C. −0,27.
D. 0,54.
Cho hàm số f x = 12 x ≥ 9 a x − 2 b − 12 x − 1 3 − 2 x < 9 . Biết rằng a, b là giá trị thực để hàm số liên tục tại x 0 = 9. Tính giá trị của P = a + b
A. P = 1 2
B. P = 5
C. P = 17
D. P = − 1 2
Cho hàm số f x = 2 x 3 + a x 2 − 4 x + b x − 1 2 k h i x ≠ 1 3 c + 1 khi x = 1 . Biết rằng a, b, c là giá trị thực để hàm số liên tục tại x 0 = 1. Giá trị c thuộc khoảng nào sau đây?
A. c ∈ 0 ; 1
B. c ∈ 1 ; 2
C. c ∈ 2 ; 3
D. c ∈ 3 ; 4
Cho hàm số y= 2 x + 1 1 3 + m 2 + m (m là tham số). Biết rằng có hai giá trị m 1 ; m 2 để giá trị lớn nhất của hàm số y=f(x) trên đoạn 7 12 ; 13 bằng 8. Tính .
A. T=9
B. T=4
C. T=36
D. T=25
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Biết S là tập các giá trị thực của m để hàm số y = 2 f ( x ) + m có 5 điểm cực trị. Gọi a, b lần lượt là giá trị nguyên âm lớn nhất và giá trị nguyên dương nhỏ nhất của tập S. Tính tổng T = a + b.
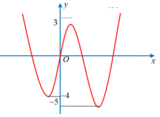
A. T = 2
B. T = 1
C. T = -1
D. T = -2
Đáp án A
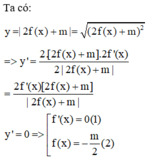
Bài toán cần 5 điểm cực trị => Tổng số nghiệm của (1) và (2) phải là 5
Đối với (1) => số nghiệm chính là số điểm cực trị. Nhìn vào đồ thị => có 3 cực trị
=> Phương trinh (2) phải có 2 nghiệm khác 3 nghiệm trên. Nhìn vào đồ thị ta thấy