Tập D = ℝ \ k π 2 k ∈ ℤ là tập xác định của hàm số nào sau đây?
A. y = cot x
B. y = cot 2 x
C. y = tan x
D. y = tan 2 x
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π/2 < α < π, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 3 là
A. π - α + k2π, k ∈ Z B. α + π/2 + k2π, k ∈ Z
C. α - π + k2π, k ∈ Z D. -α + k2π, k ∈ Z
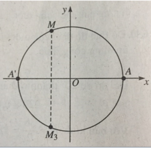
-π = -3,14; -2π = -6,28; (-5π)/2 = -7,85.
Vậy (-5π)/2 < -6,32 < -2π.
Do đó điểm M nằm ở góc phần tư thứ II.
Đáp án: B
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π < α < 3π/2, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 2 là
A. α - π + k2π, k ∈ Z B. π - α + k2π, k ∈ Z
C. 2π - α + k2π, k ∈ Z D. 3π/2 - α + k2π, k ∈ Z
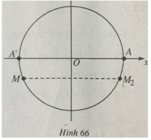
(h.66) Ta có
A M 2 = MA’ = MA + AA’
Suy ra
Sđ A M 2 = -α + π + k2π, k ∈ Z.
Vậy đáp án là B.
6.13. (h.67) Ta có
Sđ A M 3 = -sđ AM = -α + k2π, k ∈ Z.
Đáp án: D
Điều kiện để hàm số y=\frac{1+\cos x}{\sin x}y=sinx1+cosx xác định là
x\ne k\pi ,k\in ℤ.x=kπ,k∈Z.
x\ne -\pi +k2\pi ,k\in ℤ.x=−π+k2π,k∈Z.
x\ne \frac{\pi }{2}+k\pi ,k\in ℤ.x=2π+kπ,k∈Z.
x\ne \frac{\pi }{2}+k2\pi ,k\in ℤ.x=2π+k2π,k∈Z.
Bạn kiểm tra lại đề bài!
Hình như đề bài ko đúng đó bn!..bn kiểm tra lại
Cho tập hợp X={2n+1} π, với n là số nguyên. Và tập Y = {4k ±1} π, với k là số nguyên. Mối quan hệ của X và Y là:
(1) Cho tập hợp X={2n+1} π, với n là số nguyên. Và tập Y = {4k ±1} π, với k là số nguyên. Mối quan hệ của X và Y là:
A. X ⊂ Y
B. Y ⊂ X
C. X = Y
D. X ≠ Y
Cho hàm f có tập xác định là K ⊂ ℝ , đồng thời f có đạo hàm f ' x trên K. Xét hai phát biểu sau:
(1) Nếu f ' x 0 ≠ 0 thì x 0 không là điểm cực trị của hàm f trên K.
(2) Nếu x 0 mà f ' x có sự đổi dấu thì x 0 là điểm cực trị của hàm f.
Chọn khẳng định đúng
A. (1), (2) đều đúng.
B. (1), (2) đều sai
C. (1) sai, (2) đúng.
D. (1) đúng, (2) sai
Đáp án D
(1) Nếu f ' x 0 = 0 hoặc f ' x 0 không xác định trên K thì x 0 có thể là điểm cực trị của hàm số trên K. Còn nếu f ' x 0 ≠ 0 thì x 0 không thể nào là điểm cực trị của hàm số trên K. Vậy phát biểu (1) đúng.
(2) Nếu x 0 ∉ K mà qua điểm x 0 , f ' x có sự đổi dấu thì x 0 không phải là điểm cực trị của hàm số f. Vậy phát biểu (2) sai.
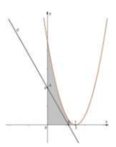
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y = x 2 − 6 x + 9 và 2 đường thẳng x = 0, y = 0. Đường thẳng (d) có hệ số k ( k ∈ ℝ ) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
A. − 16 9 .
B. 1 9 .
C. − 1 12 .
D. − 1 18 .
Đáp án A
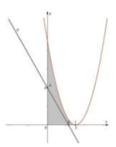
Phương trình hoành độ giao điểm của đồ thị hàm số y = x 2 − 6 x + 9 và trục hoành là:
x 2 − 6 x + 9 = 0 ⇔ x = 0 .
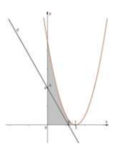
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = x 2 − 6 x + 9 và 2 đường thẳng x= 0; y = 0 là:
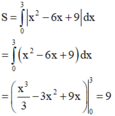
Phương trình đường thẳng (d) có hệ số góc k và cắt trục tung tại điểm A(0;4) là: y = kx +4
Gọi B là giao điểm của (d) và trục hoành ⇒ B − 4 k ; 0 .
Để (d) chia (H) thành 2 phần có diện tích bằng nhau thì:
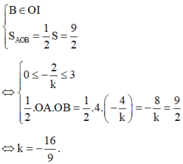 .
.
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y = x 2 − 6 x + 9 và 2 đường thẳng x = 0, y = 0. Đường thẳng (d) có hệ số k ( k ∈ ℝ ) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
A. − 16 9 .
B. 1 9 .
C. − 1 12 .
D. − 1 18 .
Đáp án A
Phương trình hoành độ giao điểm của đồ thị hàm số y = x 2 − 6 x + 9 và trục hoành là:
x 2 − 6 x + 9 = 0 ⇔ x = 0 .
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = x 2 − 6 x + 9 và 2 đường thẳng x= 0; y = 0 là:
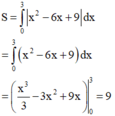
Phương trình đường thẳng (d) có hệ số góc k và cắt trục tung tại điểm A(0;4) là: y = kx +4
Gọi B là giao điểm của (d) và trục hoành ⇒ B − 4 k ; 0 .
Để (d) chia (H) thành 2 phần có diện tích bằng nhau thì:
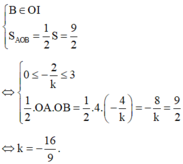
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y = x 2 − 6 x + 9 và 2 đường thẳng x = 0, y = 0. Đường thẳng (d) có hệ số k ( k ∈ ℝ ) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
A. − 16 9 .
B. 1 9 .
C. − 1 12 .
D. − 1 18 .
Đáp án A
Phương trình hoành độ giao điểm của đồ thị hàm số y = x 2 − 6 x + 9 và trục hoành là:
x 2 − 6 x + 9 = 0 ⇔ x = 0 .
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = x 2 − 6 x + 9 và 2 đường thẳng x= 0; y = 0 là:
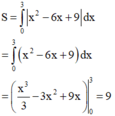
Phương trình đường thẳng (d) có hệ số góc k và cắt trục tung tại điểm A(0;4) là: y = kx +4
Gọi B là giao điểm của (d) và trục hoành ⇒ B − 4 k ; 0 .
Để (d) chia (H) thành 2 phần có diện tích bằng nhau thì:
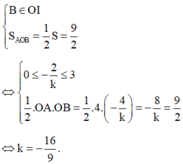
Cho hàm f có tập xác định là K ⊂ ℝ , đồng thời f có đạo hàm f'(x) trên K . Xét hai phát biểu sau:
(1) Nếu f ' x 0 ≠ 0 thì x 0 không là điểm cực trị của hàm f trên K.
(2) Nếu qua x 0 mà f'(x) có sự đổi dấu thì x 0 là điểm cực trị của hàm f.
Chọn khẳng định đúng.
A. (1), (2) đều đúng.
B. (1),(2) đều sai.
C. (1) sai, (2) đúng.
D. (1) đúng, (2) sai
Đáp án D
(2) sai vì xảy ra trường hợp x 0 không thuộc K . Ví dụ hàm
![]()