Đáp án B
TXĐ của hàm y = tanx là D = ℝ \ π 2 + k π | k ∈ ℤ nên TXĐ của hàm y = tan 2 x là D = ℝ \ π 4 + k π 2 | k ∈ ℤ
TXĐ của hàm y = cot x là D = ℝ \ k π | k ∈ ℤ nên TXĐ của hàm y = cot 2 x là D = ℝ \ k π 2 | k ∈ ℤ
Đáp án B
TXĐ của hàm y = tanx là D = ℝ \ π 2 + k π | k ∈ ℤ nên TXĐ của hàm y = tan 2 x là D = ℝ \ π 4 + k π 2 | k ∈ ℤ
TXĐ của hàm y = cot x là D = ℝ \ k π | k ∈ ℤ nên TXĐ của hàm y = cot 2 x là D = ℝ \ k π 2 | k ∈ ℤ
Trong các hàm số y = tan x ; y = sin 2 x ; y = sin x ; y = c o t x có bao nhiêu hàm số thỏa mãn tính chất f x + k π = f x ; ∀ x ∈ ℝ ; k ∈ ℤ
A. 3
B. 2
C. 1
D. 4
Cho hàm số y=f(x) xác định và liên tục trên tập D = ℝ \ { - 1 } và có bảng biến thiên:
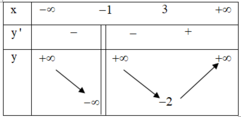
Dựa vào bảng biến thiên của hàm số y=f(x) Khẳng định nào sau đây là khẳng
định sai?
A. Giá trị nhỏ nhất của hàm số trên đoạn [ 1 ; 8 ] bằng -2
B. Phương trình f(x)=m có 3 nghiệm thực phân biệt khi x > -2
C. Hàm số đạt cực tiểu tại x=3
D. Hàm số nghịch biến trên khoảng ( - ∞ ; 3 )
Tập xác định của hàm số: y = cot x là:
A. D = ℝ \ k π 2 | k ∈ ℤ .
B. D = ℝ \ kπ | k ∈ ℤ .
C. D = ℝ \ π 4 + kπ | k ∈ ℤ .
D. D = ℝ \ π 2 + kπ | k ∈ ℤ .
Tập xác định của hàm số y = cot x là
A. D = ℝ \ k π 2 k ∈ ℤ
B. D = ℝ \ k π k ∈ ℤ
C. D = ℝ \ k 2 π k ∈ ℤ
D. D = ℝ \ π 2 + k π k ∈ ℤ
Tập xác định của hàm số y = c o t x là
A. D = ℝ \ k π 2 k ∈ ℤ
B. D = ℝ \ k π k ∈ ℤ
C. D = ℝ \ k 2 π k ∈ ℤ
D. D = ℝ \ π 2 + k π k ∈ ℤ
Cho hàm số y = f ( x ) xác định và liên tục trên tập D = ℝ \ 1 và có bảng biến thiên
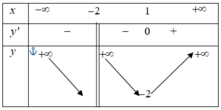
Dựa vào bảng biến thiên của hàm số y = f x . Khẳng định nào sau đây là sai?
A. Phương trình f x = m có 3 nghiệm thực phân biệt khi x > -2
B. Giá trị nhỏ nhất của hàm số trên đoạn 0 ; 6 là -2
C. Hàm số đạt cực tiểu tại x = 1
D. Hàm số nghịch biến trên khoảng − ∞ ; 1
Cho hàm số y = ( x - 2 ) - 1 2 Bạn Toán tìm tập xác định của hàm số bằng cách như sau:
Bước 1: Ta có y = 1 ( x - 2 ) 1 2 = 1 x - 2
Bước 2: Hàm số xác định ⇔ x - 2 > 0 ⇔ x > 2
Bước 3: Vậy tập xác định của hàm số là D = ( 2 ; + ∞ )
Lời giải trên của bạn toán đúng hay sai? Nếu sai thì sai ở bước nào?
A. Bước 3
B. Bước 1
C. Đúng
D. Bước 2
Một học sinh khảo sát sự biến thiên của hàm số như sau:
I. Tập xác định: D = ℝ
II. Sự biến thiên: y ' = x 2 − x − 2 ; y ' = 0 ⇔ x = − 1 x = 2
lim x → − ∞ y = − ∞ ; lim x → + ∞ y = + ∞
III. Bảng biến thiên:
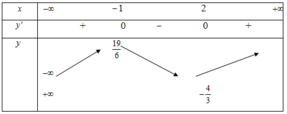
IV. Vậy hàm số đồng biến trên nghịch biến trên khoảng
−
∞
;
−
1
∪
2
;
+
∞
, nghịch biến trên khoảng
−
1
;
2
Lời giải trên sai từ bước nào?
A. Bước IV
B. Bước I
C. Bước II
D. Bước III
Cho hàm số y = x + 3 e − 5 − x 6 , Gọi D là tập xác định của hàm số, khẳng định nào sau đây đúng?
A. D = − 3 ; + ∞
B. D ⊂ − 3 ; 5
C. D ⊂ − 3 ; 5
D. D = − 3 ; + ∞ \ 5