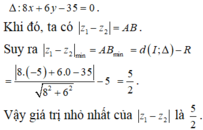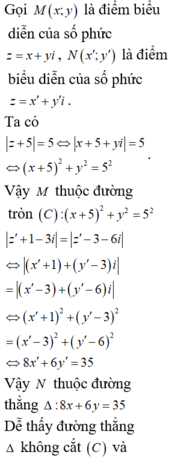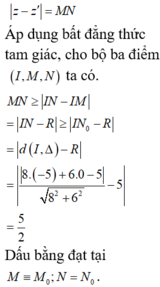Giá trị nhỏ nhất của Ix2+3I+Iy2+6I-12,5 là......

Những câu hỏi liên quan
Cho hai số phức
z
1
;
z
2
thỏa mãn
z
1
+
5
5
;
z
1
+
1
-
3
i
z...
Đọc tiếp
Cho hai số phức z 1 ; z 2 thỏa mãn z 1 + 5 = 5 ; z 1 + 1 - 3 i = z 2 - 3 - 6 i . Giá trị nhỏ nhất của z 1 - z 2 là
A. 5 2
B. 7 2
C. 1 2
D. 3 2
Cho hai số phức u, v thỏa mãn
3
u
-
6
i
+
3
u
-
1
-
3
i
5
10
,
v
-
1
+
2
i...
Đọc tiếp
Cho hai số phức u, v thỏa mãn 3 u - 6 i + 3 u - 1 - 3 i = 5 10 , v - 1 + 2 i = v ¯ + i . Giá trị nhỏ nhất của u - v là:
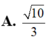
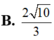
![]()
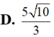
Cho hai số phức
z
1
,
z
2
thỏa mãn
z
1
+
2
2
và
z
2
-
3
i
z
2
+
1
-
6
i
. Tì...
Đọc tiếp
Cho hai số phức z 1 , z 2 thỏa mãn z 1 + 2 = 2 và z 2 - 3 i = z 2 + 1 - 6 i . Tìm giá trị nhỏ nhất của z 1 + z 2 .
A. - 10 + 6 10 5
B. 10 + 6 10 5
C. 0
D. 12 10
Đáp án A
Đặt z 1 = x + y i , z 2 = a + b i với x , y , a , b ∈ R . Ta có:
+ z 1 + 2 = 2 ⇔ x + 2 + y i = 2 ⇔ x + 2 2 + y 2 = 4
⇒ Tập hợp điểm biểu diễn số phức z 1 là điểm M(x;y) thuộc (C) có tâm I(-2;0) và bán kính R = 2
+ z 2 - 3 i = z 2 + 1 - 6 i ⇔ a + ( b - 3 ) i = a + 1 + b - 6 i
a 2 + ( b - 3 ) 2 = ( a + 1 ) 2 + ( b - 6 ) 2 ⇔ a - 3 b + 4 = 0
⇒ Điểm biểu diễn số phức z 2 là N ∈ d : x - 3 y + 14 = 0
+ Có
z 1 - z 2 = x - a + y + b i = x - a 2 + y - b 2 = M N ⇒ z 1 - z 2 m i n = M N m i n
⇒ Tìm M, N lần lượt thuộc (C) và d sao cho M N m i n
Ta có d I , d = 12 10 > R ⇒ d không cắt (C)
M N m i n = d I , d - R = 12 10 - 2 = - 10 + 6 10 5
Đúng 0
Bình luận (0)
Cho hai số phức
z
1
,
z
2
thỏa mãn
z
1
+
2
2
và
z
2
−
3
i
z
2...
Đọc tiếp
Cho hai số phức z 1 , z 2 thỏa mãn z 1 + 2 = 2 và z 2 − 3 i = z 2 + 1 − 6 i . Tìm giá trị nhỏ nhất của z 1 − z 2
A. − 10 + 6 10 5
B. 10 + 6 10 5
C. 0
D. 12 10
Cho hai số thực
z
1
,
z
2
thỏa mãn
z
1
+
5
5
và
z
2...
Đọc tiếp
Cho hai số thực z 1 , z 2 thỏa mãn z 1 + 5 = 5 và z 2 + 1 - 3 i = z 2 - 3 - 6 i . Tìm giá trị nhỏ nhất của z 1 - z 2
A. 5 2
B. 5 4
C. 10
D. 3
Chọn đáp án A
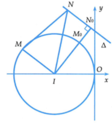
Giả sử z 1 = x 1 + y 1 i có điểm biểu diễn là M x 1 ; y 1 và z 2 = x 2 + y 2 i có điểm biểu diễn là N x 2 ; y 2
Từ giả thiết ta có
![]()
![]()
Suy ra tập hợp các điểm M là đường tròn (C): x + 5 2 + y 2 = 25
![]()
![]()
![]()
![]()
Suy ra tập hợp các điểm N là đường thẳng d: 8x +6y -35 = 0
Ta thấy đường thẳng d không cắt đường tròn (C) và z 1 - z 2 = M N
Áp dụng bất đẳng thức tam giác cho bộ ba điểm (I ,M, N) ta có
![]()
với N 0 là hình chiếu của I trên d
Khi đó
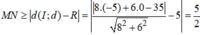
Dấu “=” xảy ra khi và chỉ khi N ≡ N 0 và M ≡ M 0 , với M 0 là giao điểm của đoạn thẳng I N 0 với đường tròn (C).
Đúng 0
Bình luận (0)
Cho hai số phức z,z thỏa mãn
|
z
+
5
|
5
và
|
z
+
1
-
3
i
|
|
z
-
3
-
6
i
|
. Tìm giá trị nhỏ nhất của
|
z
-
z
|
.
Đọc tiếp
Cho hai số phức z,z' thỏa mãn | z + 5 | = 5 và | z ' + 1 - 3 i | = | z ' - 3 - 6 i | . Tìm giá trị nhỏ nhất của | z - z ' | .
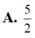
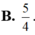
![]()
![]()
Giá trị nhỏ nhất của A= I-x+7/3I+I-x-11/3I-17 là
Tìm giá trị nhỏ nhất của A= Ix-1,5I-7,5+I2x-3I
chú ý: I là giá trị tuyệt đối
Ta có \(\hept{\begin{cases}\left|x-1,5\right|\ge0\forall x\\\left|2x-3\right|\ge0\forall x\end{cases}}\Rightarrow\left|x-1,5\right|+\left|2x-3\right|-7\ge-7\forall x\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x-1,5=0\\2x-3=0\end{cases}\Rightarrow\hept{\begin{cases}x=1,5\\x=1,5\end{cases}}\Rightarrow x=1,5}\)
Vậy GTNN của A là - 7 khi x = 1,5
giá trị nhỏ nhất của A=Ix+1/6I