Có bao nhiêu giá trị nguyên của tham số thực m để hàm số y = m - 1 x 3 + m - 1 x 2 + x + m đồng biến trên ℝ ?
A. 5.
B. 3.
C. 2.
D. 4.
Cho hàm số y = 4 3 x 3 + 4 x 2 = m x + 10 (1) với m là tham số thực. Có tất cả bao nhiêu giá trị nguyên của tham số thực m lớn hơn -10 để hàm số (1) đồng biến trên khoảng - ∞ ; 0
A. 5
B. 4
C. 6
D. 7
Cho hàm số f ( x ) = m - 2 x 3 - 2 2 m - 3 x 2 + 5 m - 3 x - 2 m - 2 với m là tham số thực. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f x có 5 điểm cực trị?
A. 0.
B. 3.
C. 2.
D. 1.
Hàm số y = f x với f(x) là hàm đa thức bậc 3 có 5 điểm cực trị khi và chỉ khi hàm số f(x) có hai cực trị và đồ thị của hàm số cắt trục hoành tại 3 điểm phân biệt.
Mặt khác, f(x) là hàm số bậc 3 nên khi đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt thì hàm số đồng thời cũng có hai cực trị. Do đó ta chỉ cần tìm điều kiện để phương trình f(x) = 0 có 3 nghiệm phân biệt.

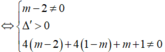
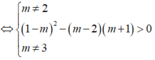
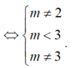

Chọn D
Có bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn - 2018 ; 2018 để hàm số y = x 3 - 6 x + m x + 1 đồng biến trên 1 ; + ∞
A. 2007
B. 2030
C. 2005
D. 2018
3. Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y=\dfrac{x+1}{x+3m}\) nghịch biến trên khoảng(6;+\(\infty\) )?
4. Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y=\dfrac{x+2}{x+3m}\) đồng biến trên khoảng (-\(\infty\);-6)?
3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)
Có tất cả bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn [-281;2018] để hàm số y = x 3 - 6 x 2 + m x + 1 đồng biến trên khoảng (1;+∞).
A. 2007.
B. 2030.
C. 2005.
D. 2018.
Có bao nhiêu giá trị nguyên của tham số thực m thuộc khoảng (-10000;10000) để hàm số y = 2 x 3 - 3 ( 2 m + 1 ) x 2 + 6 m ( m + 1 ) x + 1 đồng biến trên khoảng ( 2 ; + ∞ ) ?
A. 999.
B. 1001.
C. 1998.
D. 1000.
Chọn B
Phương pháp:
Tính y'.
Tìm m để ![]()
Cách giải:
Ta có ![]()
![]()
Xét phương trình y' = 0 ![]() có
có ![]()
Suy ra phương trình y' = 0 luôn có hai nghiệm ![]()
Dễ thấy ![]() trong khoảng
trong khoảng ![]() thì hàm số đồng biến.
thì hàm số đồng biến.
Bài toán thỏa ![]()
Do ![]()
![]()
Vậy có ![]() giá trị của m thỏa mãn bài toán.
giá trị của m thỏa mãn bài toán.
Chú ý:
Cách khác: Tìm m để ![]()
Theo định lí Viet, ta có 
Hàm số đồng biến trên
(
2
;
+
∞
)
⇔
phương trình y' = 0 có hai nghiệm ![]()
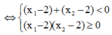
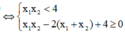

![]()
![]()
Vậy có 1001 số nguyên m thuộc khoảng (-10000;10000)
Có bao nhiêu giá trị nguyên của tham số thực m thuộc khoảng (-1000;1000) để hàm số y = 2 x 3 - 3 ( 2 m + 1 ) x 2 + 6 m ( m + 1 ) x + 1 đồng biến trên khoảng ( 2 ; + ∞ ) ?
A. 999.
B. 1001.
C. 1998
D. 1000.
Cho hàm số y=x4-2mx2+2 với m là tham số thực. Có bao nhiêu giá trị nguyên của m để đồ thị hàm số có ba điểm cực trị A; B; C thỏa mãn OA.OB.OC=12?
A.2
B.1
C.0
D.4
Để hàm số có ba điểm cực trị khi và chỉ khi ab< 0 hay 1.( -2m) <0
Suy ra m> 0
Khi đó
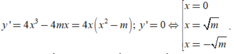
Suy ra tọa độ các điểm cực trị của đồ thị hàm số là:
A 0 ; 2 , B m ; - m 2 + 2 , C - m ; - m 2 + 2
Ycbt O A . O B . O C = 12 ⇔ 2 m + - m 2 + 2 2 = 12
Giải ra ta được m=2; có một giá trị nguyên.
Chọn B.
Có bao nhiêu giá trị nguyên của tham số thực m thuộc khoảng - 1000 ; 1000 để hàm số y = 2 x 3 - 3 2 m + 1 x 2 + 6 m m + 1 x + 1 đồng biến trên khoảng 2 ; + ∞ ?
A. 999
B. 1001
C. 1998
D. 998
Ta có:
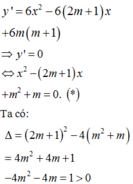
⇒ * luôn có hai nghiệm phân biệt x 1 ; x 2 x 1 < x 2 với mọi m.
Áp dụng hệ thức Vi-ét ta có:
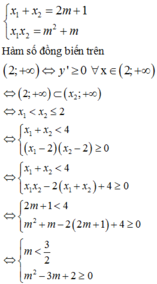
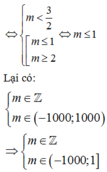
Vậy có tất cả 1001 giá trị m thỏa mãn bài toán.
Chọn B.