Cho hình chóp S.ABCD có S A ⊥ A B C D , SA=2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC
A. a 2 4
B. a 3 3
C. a 3 4
D. a 2 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh, tam giác SAB cân tại S. SA=SB=2a, (SAB) \(\perp\) (ABCD)
a, Tính (SD,(ABCD))
b, (SH, (SCD)) với H là trung điểm của
c, (SC, (SAB))
d, (SA, (SBC))
Hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mp(ABCD), SA = 2a . Diện tích mặt cầu ngoại tiếp hình chóp S.ABCD bằng:
A. 2 πa 2
B. πa 2
C. 3 πa 2
D. 6 πa 2
Hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mp(ABCD), S A = 2 a . Diện tích mặt cầu ngoại tiếp hình chóp S.ABCD bằng:
A. 2 π a 2
B. π a 2
C. 3 π a 2
D. 6 π a 2
Đáp án D
Ta có R = S A 2 4 + R d 2 = a 2 + a 2 2 2 = a 3 2 ⇒ S = 4 π R 2 = 6 π a 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt đáy (ABCD), SA=2a. Tính theo a thể tích khối chóp S.ABCD
A. a 3 3
B. a 3 6
C. a 3 4
D. 2 a 3 5
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D với AD = 2a, AB = 2DC = 2a, SA ⊥ (ABCD) và cạnh SB tạo với đáy một góc 600. Thể tích khối chóp S.ABCD bằng
A. 2 a 3 3 3
B. a 3 3
C. 2 a 3 3
D. a 3
Phương pháp
+ Xác định góc giữa đường thẳng d và mặt phẳng (P) là góc giữa đường thẳng d và đường thẳng d' với d' là hình chiếu của d trên mặt phẳng (P).
+ Thể tích hình chóp có chiều cao h và diện tích đáy S là V = 1 3 h S
Cách giải:
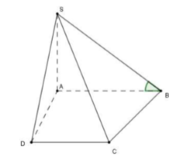
+ Ta có SA ⊥ (ABCD) => AB là hình chiếu của
SB lên mặt phẳng (ABCD) . Suy ra góc giữa SB và đáy là góc ∠ SBA = 600.
+ Xét tam giác vuông SAB có: ![]()
+ Diện tích đáy
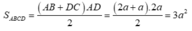
+ Thể tích khối chóp là
![]()
Chọn C.
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D với AD = 2a, AB = 2DC = 2a, S A ⊥ A B C D và cạnh SB tạo với đáy một góc 60 ° . Thể tích khối chóp S.ABCD bằng
A. 2 a 3 3 3
B. a 3 3
C. 2 a 3 3
D. a 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA ⊥ (ABCD) và SA = a. Gọi E là trung điểm của cạnh AB. Diện tích mặt cầu ngoại tiếp hình chóp bằng .SBCE
A. 14 πa 2
B. 11 πa 2
C. 8 πa 2
D. 12 πa 2
Đáp án A
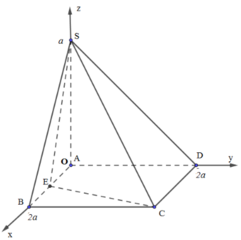
Phương pháp:
Sử dụng phương pháp tọa độ hóa.
Cách giải:
Gắn hệ trục tọa độ như hình vẽ.
Trong đó, B(2a;0;0), C(2a;2a;0), E(a;0;0), S(0;0;a)
Gọi I(x0;y0;z0) là tâm của mặt cầu ngoại tiếp hình chóp S.BEC. Khi đó, IS2 = IB2 = IC2 = IE2
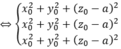
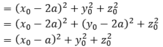
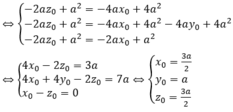
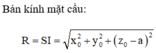
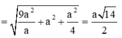
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a và SA vuông góc với đáy, SA=2a Tính theo a thể tích khối chóp S.ABCD
![]()
![]()
![]()

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; S A ⊥ A B C D và SA=2a. Tính khoảng cách d từ điểm B đến mặt phẳng (SCD)
A. d = a 5 5 .
B. d = a
C. d = 4 a 5 5 .
D. d = 2 a 5 5 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; S A ⊥ A B C D và S A = 2 a . Tính khoảng cách d từ điểm B đến mặt phẳng (SCD).
A. d = a 5 5 .
B. d = a .
C. d = 4 a 5 5 .
D. d = 2 a 5 5 .
Đáp án D
Cách 1: Tư duy tự luận (Tính khoảng cách dựa vào hình chiếu)

Ta có
A B // C D A B ⊄ S C D C D ⊂ S C D ⇒ A B // S C D ⇒ d B , S C D = d A ; S C D
Lại có C D ⊥ A D , A D ⊂ S A D C D ⊥ S A , S A ⊂ S A D A D ∩ S A = A ⇒ C D ⊥ S A D .
Trong mặt phẳng (SAD) : Kẻ A H ⊥ S D , H ∈ S D thì C D ⊥ A H .
Suy ra A H ⊥ A C D ⇒ A H = d A ; S C D = d B ; S C D .
Δ S A D vuông tại A nên
1 A H 2 = 1 S A 2 + 1 A D 2 = 1 2 a 2 + 1 a 2 = 5 4 a 2 ⇒ A H = 2 a 5
Vậy khoảng cách từ điểm B đến mặt phẳng (SCD) là d = 2 a 5 5 .
Cách 2: Tư duy tự luận (Tinh khoảng cách qua công thức thể tích)
Thể tích khối chóp S.ABCD là V S . A B C D = 1 3 S A . S A B C D = 1 3 .2 a . a 2 = 2 a 3 3 (đvtt)
Do S Δ B C D = 1 2 S A B C D ⇒ V S . B C D = 1 2 V S . A B C D = a 3 3 (đvtt).
Ta có C D ⊥ S A D (xem lại phần chứng minh ở cách 1) ⇒ C D ⊥ S D ⇒ Δ S C D vuông tại D. Suy ra
S Δ S C D = 1 2 S D . C D = 1 2 S A 2 + A D 2 . C D = 1 2 . a . 2 a 2 + a 2 = a 2 5 2
(đvdt)
Mặt khác
V S . B C D = V B . S C D = 1 3 d B ; S C D . S Δ S C D ⇒ d B ; S C D = 3 V S . B C D S Δ S C D = 2 a 5
Vậy khoảng cách từ điểm B đến mặt phẳng (SCD) là d = 2 a 5 5 .