Cho số phức z=2+3i. Module số phức w = ( 3 - 2 z ¯ ) ( z + 1 ) - i là
A. 3 15
B. 7 13
C. 6 7
D. 123
Cho số phức z thỏa mãn z - 1 - i = 1 , số phức w thỏa mãn w ¯ - 2 - 3 i = 2 . Tìm giá trị nhỏ nhất của z - w .
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn z − 1 − i = 1 , số phức w thỏa mãn w ¯ − 2 − 3 i = 2 . Tìm giá trị nhỏ nhất của z − w .
A. 17 + 3
B. 13 + 3
C. 13 - 3
D. 17 - 3
Cho số phức z thỏa mãn z - 1 - i = 1 , số phức w thỏa mãn w ¯ - 2 - 3 i = 2 . Tính giá trị nhỏ nhất của z - w .
A. 13 - 3
B. 17 - 3
C. 17 + 3
D. 13 + 3
Cho các số phức z thỏa mãn |z2 + 4| = 2|z|. Kí hiệu M = max|z| và m = min|z|. Tìm module của số phức w = M + m?
![]()
![]()
![]()
![]()
Chọn A.
Ta có ![]()
Giải bất phương trình trên với ẩn |z| ta được:
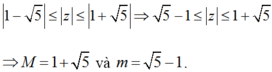
Vậy ![]()
Cho số phức z=2+3i. Điểm biểu diễn của số phức z' đối xứng với số phức w=2z-3i qua Ox là:
A. (4;3)
B. (-4;3)
C. (-4;-3)
D. (4;-3)
Cho số phức z, biết ( 2 z - 1 ) ( 1 + i ) + ( z ¯ + 1 ) ( 1 - i ) = 2 - 2 i .
Tìm số phức liên hợp của số phức w=3z-3i
A. 1 3 - 1 3 i
B. 1 3 + 1 3 i
C. 1 - 4 i
D. 1 + 4 i
Chọn D.
Giả sử z=a+bi với a,b ∈ ℝ
Thay vào biểu thức ta được:
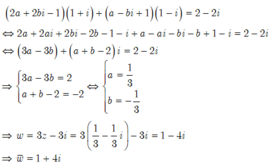
Cho | z - 4 + 3 i | = 3 . Số phức z có module nhỏ nhất có phần thực bằng?
A. 8 5
B. - 6 5
C. - 8 5
D. 6 5
Chọn A.
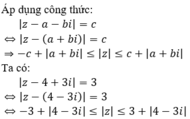
![]()
![]()
+ Tìm Số phức z có module nhỏ nhất là:

\(M\left(1;1\right)\) ; \(N\left(2;3\right)\)
Gọi \(w=x+yi\Rightarrow Q\left(x;y\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{MN}=\left(1;2\right)\\\overrightarrow{MQ}=\left(x-1;y-1\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MN}+3\overrightarrow{MQ}=\left(3x-2;3y-1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\) \(\Rightarrow w=\dfrac{2}{3}+\dfrac{1}{3}i\)
Cho số phức z thỏa mãn |z| = 5 và |z + 3| = |z + 3 - 10i| .Tính số phức w=z-4+3i
A. W=-4+8i
B. w=1=3i
C. w= -1+7i
D. w=-3+8i