Biết rằng khi tham số thực m ≠ − 1 thì các đường cong C m : y = 2 x 2 + 1 + m x + 1 + m m − x luôn tiếp xúc một và chỉ một đường thẳng Δ cố định. Tính khoảng cách d từ điểm K(2;5) đến Δ
A. d = 2
B. d = 3 2
C. d = 2 2
D. d = 7 2
Những câu hỏi liên quan
Cho hàm số
y
x
3
−
3
x
2
−
m
2
−
2
x
+
m
2
có đồ thị là đường cong
C
. Biết rằng các số thực
m
1
;
m
2...
Đọc tiếp
Cho hàm số y = x 3 − 3 x 2 − m 2 − 2 x + m 2 có đồ thị là đường cong C . Biết rằng các số thực m 1 ; m 2 của tham số m để hai điểm cực trị của C và giao điểm của C với trục hoành tạo thành 4 đỉnh của hình chữ nhật. Tính T = m 1 4 + m 2 4
A. T = 22 − 12 2
B. T = 11 − 6 2
C. T = 3 2 − 2 2
D. T = 15 − 6 2 2
Đáp án B
Ta có: y ' = 3 x 2 − 6 x − m 2 + 2
Lấy y y ' thì phần dư ta được PT đường thẳng qua các điểm cực trị là:
y = 2 3 x m 2 + 1 + 2 m 2 + 2 3
Phương trình hoành độ giao điểm là: x 3 − 3 x 2 − m 2 − 2 x + m 2 = 0 ⇔ x 3 − 3 x 2 + 2 x − m 2 x − 1 = 0 ⇔ x − 1 x 2 − 2 x − m 2 = 0 ⇔ x = 1 g x = x 2 − 2 x − m 2 = 0
Đk cắt tại 3 điểm phân biệt ⇔ Δ ' = 1 + m 2 > 0 g ' 1 = − 1 − m 2 ≠ 0
Khi đó C cắt Ox tại 3 điểm A x 1 ; 0 ; B 1 ; 0 ; C x 2 ; 0 , theo Viet ta có: x 1 + x 2 = 2 = 2 x B
Gọi M và N là tọa độ 2 điểm cực trị thì B là trung điểm của MN (Do B là điểm uốn)
Để A M C N là hình chữ nhật thì A C = M N ⇔ x 1 − x 2 = x M − x N 2 + 4 9 m 2 + 1 2 x M − x N 2
Trong đó x M + x N = 2 x M x N = 2 − m 2 3 ⇒ 4 + 4 m 2 = 4 + 4 m 2 − 8 3 4 9 m 2 + 1 2 + 1 ⇔ m 2 + 1 2 = 9 2
m 2 = 3 2 − 1 m 2 = − 3 2 − 1 ⇔ m = ± 3 2 − 1
Do đó T = m 1 4 + m 2 4 = 11 − 6 2
Đúng 0
Bình luận (0)
Cho hàm số có đồ thị là đường cong (C). Biết rằng tồn tại hai số thực
m
1
,
m
2
của tham số m để hai điểm cực trị của (C) và hai giao điểm của (C) với trục hoành tạo thành bốn đỉnh của một hình chữ nhật. Tính . A. B. C. D.
Đọc tiếp
Cho hàm số 
có đồ thị là đường cong (C). Biết rằng tồn tại hai số thực
m
1
,
m
2
của tham số m để hai điểm cực trị của (C) và hai giao điểm của (C) với trục hoành tạo thành bốn đỉnh của một hình chữ nhật. Tính 
.
A. 
B. 
C.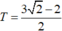 
D.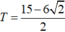 
Cho số phức
z
m
+
3
+
(
m
2
-
1
)
i
, với m là tham số thực thay đổi. Tập hợp các điểm biểu diễn số phức z thuộc đường cong (C). Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành. A.
4
3
B.
8
3
C.
2
3
D. ...
Đọc tiếp
Cho số phức z = m + 3 + ( m 2 - 1 ) i , với m là tham số thực thay đổi. Tập hợp các điểm biểu diễn số phức z thuộc đường cong (C). Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành.
A. 4 3
B. 8 3
C. 2 3
D. 1 3
Cho số phức
z
m
-
2
+
(
m
2
-
1
)
i
, với m là tham số thực thay đổi. Tập hợp các điểm biểu diễn số phức z nằm trên đường cong (C). Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành. A.
1
3
B.
8
3
C.
4
3
D. ...
Đọc tiếp
Cho số phức z = m - 2 + ( m 2 - 1 ) i , với m là tham số thực thay đổi. Tập hợp các điểm biểu diễn số phức z nằm trên đường cong (C). Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành.
A. 1 3
B. 8 3
C. 4 3
D. 2 3
Cho số phức
z
m
+
3
+
(
m
2
-
1
)
i
với m là tham số thực thay đổi. Tập hợp các điểm biểu diễn số phức z thuộc đường cong (C). Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành. A. 4/3 B. 8/3 C. 2/3 D. 1/3
Đọc tiếp
Cho số phức z = m + 3 + ( m 2 - 1 ) i với m là tham số thực thay đổi. Tập hợp các điểm biểu diễn số phức z thuộc đường cong (C). Tính diện tích hình phẳng giới hạn bởi (C) và trục hoành.
A. 4/3
B. 8/3
C. 2/3
D. 1/3
Cho hàm số yf(x) có đồ thị như đường cong trong hình bên. Tìm tất cả các giá trị thực của tham số m để phương trình
f
x
m
có 6 nghiệm phân biệt. A. -4 m -3 B. 0 m 3 C. m 4 D. 3 m 4
Đọc tiếp
Cho hàm số y=f(x) có đồ thị như đường cong
trong hình bên. Tìm tất cả các giá trị thực của tham số m để phương trình f x = m có 6 nghiệm phân biệt.
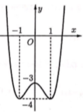
A. -4 < m < -3
B. 0 < m < 3
C. m > 4
D. 3 < m < 4
Biết rằng đường thẳng d :y-3x+m cắt đồ thị (C):
y
2
x
+
1
x
-
1
tại hai điểm phân biệt A và B sao cho trọng tâm G của tam giác OAB thuôc đồ thị (C) với O(0;0) là gốc tọa độ. Khi đó giá trị thực của tham số m thuộc tập hợp nào sau đây? A.
(
2
;
3
]
B. ...
Đọc tiếp
Biết rằng đường thẳng d :y=-3x+m cắt đồ thị (C): y = 2 x + 1 x - 1 tại hai điểm phân biệt A và B sao cho trọng tâm G của tam giác OAB thuôc đồ thị (C) với O(0;0) là gốc tọa độ. Khi đó giá trị thực của tham số m thuộc tập hợp nào sau đây?
A. ( 2 ; 3 ]
B. ( 5 ; - 2 ]
C. 3 : + ∞
D. ( - ∞ ; - 5 ]
Cho hàm số yf(x) có đồ thị là đường cong trong hình dưới đây. Tìm tất cả các gía trị thực của tham số m để phương trình
f
(
x
)
m
có hai nghiệm phân biệt
Đọc tiếp
Cho hàm số y=f(x) có đồ thị là đường cong trong hình dưới đây. Tìm tất cả các gía trị thực của tham số m để phương trình f ( x ) = m có hai nghiệm phân biệt
Biết rằng đồ thị (C) của hàm số
y
2
x
+
1
x
+
2
luôn cắt đường thẳng
d
:
y
-
x
+
m
tại hai điểm phân biệt A và B. Tìm các giá trị thực của tham số m sao cho độ dài đoạn thẳng AB ngắn nhất A. m 1 B.
m...
Đọc tiếp
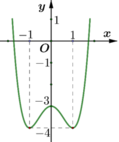
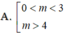
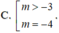
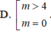
Biết rằng đồ thị (C) của hàm số y = 2 x + 1 x + 2 luôn cắt đường thẳng d : y = - x + m tại hai điểm phân biệt A và B. Tìm các giá trị thực của tham số m sao cho độ dài đoạn thẳng AB ngắn nhất
A. m = 1
B. m = 2 3
C. m = 4
D. m = 0
