Cho số phức z = 1 – 2i. Tính z
A. 5
B. 5
C. 3
D. 2
Những câu hỏi liên quan
Cho số phức Z thoả mãn (1+2i)z-5= 3i tìm số phức liên hợp z 2/ cho số phức z=a+bi(a, b thuộc R) thoả mãn 3z-5z ngan -6+10i=0 .tính a-b
\(\left(1+2i\right)z-5=3i\Leftrightarrow\left(1+2i\right)z=5+3i\)
\(\Rightarrow z=\dfrac{5+3i}{1+2i}=\dfrac{11}{5}-\dfrac{7}{5}i\)
\(\Rightarrow\overline{z}=\dfrac{11}{5}+\dfrac{7}{5}i\)
2.
Đề câu này là: \(3z-5\overline{z}-6+10i=0\) đúng không nhỉ?
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn |z + 3| = 5 và |z - 2i| = |z - 2 - 2i|. Tính |z|
A. |z| = 17
B. |z| = 17
C. |z| = 10
D. |z| = 10
Cho số phức za+bi
a
,
b
∈
R
thỏa mãn
z
5
và
z
(
2
+
i
)
(
1
-
2
i
)
là một số thực. Tính
P
a
+
b...
Đọc tiếp
Cho số phức z=a+bi a , b ∈ R thỏa mãn z = 5 và z ( 2 + i ) ( 1 - 2 i ) là một số thực. Tính P = a + b .
A. P=5
B. P=7
C. P=8
D. P=4
Bài tập số 4: Tìm số phức liên hợp overline{Z} và tính modun (|z|) của số phức sau. a, z 2 + 3i b, zleft(2+3iright)^3 c, zdfrac{2+3i}{1-2i} d, zsqrt{2}-dfrac{4}{3}i
Đọc tiếp
Bài tập số 4: Tìm số phức liên hợp \(\overline{Z}\) và tính modun (|z|) của số phức sau.
a, z = 2 + 3i b, \(z=\left(2+3i\right)^3\)
c, \(z=\dfrac{2+3i}{1-2i}\) d, \(z=\sqrt{2}-\dfrac{4}{3}i\)
Cho số phức z thỏa mãn
z
2
-
2
z
+
5
(
z
-
1
+
2
i
)
(
z
+
3
i
-...
Đọc tiếp
Cho số phức z thỏa mãn z 2 - 2 z + 5 = ( z - 1 + 2 i ) ( z + 3 i - 1 ) .Tính m i n w , với w = z - 2 + 2 i .
A. m i n w = 3 2
B. m i n w = 2
C. m i n w = 1
D. m i n w = 1 2
Cho số phức z thỏa mãn
z
2
-
2
z
+
5
(
z
-
1
+
2
i
)
(
z
+...
Đọc tiếp
Cho số phức z thỏa mãn z 2 - 2 z + 5 = ( z - 1 + 2 i ) ( z + 3 i - 1 ) .Tính min |w|, với w = z - 2 + 2 i
Cho 3 số phức
z
,
z
1
,
z
2
thỏa mãn
z
−
1
+
2
i
z
+
3
−
4
i
,
z
1...
Đọc tiếp
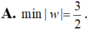
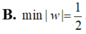
Cho 3 số phức z , z 1 , z 2 thỏa mãn z − 1 + 2 i = z + 3 − 4 i , z 1 + 5 − 2 i = 2 , z 2 − 1 − 6 i = 2. Tính giá trị nhỏ nhất của biểu thức T = z − z 1 + z − z 2 + 4
A. 2 3770 13
B. 10361 13
C. 3770 13
D. 10361 26
Câu 1 : Cho số phức z thỏa mãn z + ( 2 - i )overline{z} 3 - 5i. Môđun của số phức w z - i bằng bao nhiêu ?Câu 2 : Cho số phức z a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )z + ( 2 - i )2 4 + i. Tính P a - b
Đọc tiếp
Câu 1 : Cho số phức \(z\) thỏa mãn \(z\) + ( 2 - i )\(\overline{z}\) = 3 - 5i. Môđun của số phức w = \(z \) - i bằng bao nhiêu ?
Câu 2 : Cho số phức \(z\) = a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )\(z\) + ( 2 - i )2 = 4 + i. Tính P = a - b
Cho hai số phức
z
5
+
2
i
v
à
z
1
-
i
. Tính mô-đun của số phức
w
z
-...
Đọc tiếp
Cho hai số phức z = 5 + 2 i v à z ' = 1 - i . Tính mô-đun của số phức w = z - z '
A. 5.
B. 3 5
C. 17
D. 37
Chọn đáp án A
Ta có w = z - z ' = 4 + 3 i
⇒ w = 4 2 + 3 2 = 5
Đúng 0
Bình luận (0)
Cho hai số phức
z
5
+
2
i
và
z
1
-
i
. Tính mô-đun của số phức
w
z
-
z...
Đọc tiếp
Cho hai số phức z = 5 + 2 i và z ' = 1 - i . Tính mô-đun của số phức w = z - z '
A. 7(cm)
B. 3(cm)
C. 6(cm)
D. 2(cm)
Chọn đáp án B
Gọi các kích thước của khối hộp là a (cm), b(cm), c (cm) với a, b, c là các số nguyên dương.
Từ giả thiết ta có
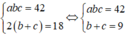
Lại có 9 = b + c ≥ 2 b c ⇒ b c ≤ 81 4
Mà b, c là các số nguyên dương nên b c ≤ 20
Từ b +c =9
⇒ trong hai số b, c có 1 số lẻ và 1 số chẵn ⇒ bc chẵn.
Từ a = 42 b c và a nguyên dương nên bc là ước nguyên dương của 42.
Nếu bc =6 thì b, c là nghiệm của phương trình X 2 - 9 X + 6 = 0 (loại vì nghiệm của phương trình này không là số nguyên).
Nếu bc =14 thì b, c là nghiệm của phương trình
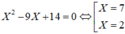
⇒ b c = 14 thỏa mãn. Vậy chiều cao của khối hộp là a = 42 b c = 3 c m
Đúng 0
Bình luận (0)