Tập xác định của hàm số y = x 4 - 2018 x 2 - 2019 là
A. - 1 ; + ∞
B. 0 ; + ∞
C. - ∞ ; 0
D. - ∞ ; + ∞
Có bao nhiêu giá trị nguyên của m thuộc khoảng (-2019; 2019) để hàm số sau có tập xác định là D = R
y = x + m + x 2 + 2 ( m + 1 ) x + m 2 + 2 m + 4 + log 2 ( x - m + 2 x 2 + 1 )
A. 2020
B. 2021
C. 2018
D. 2019
Bài 9: Cho hàm số \(y=\dfrac{2mx+4}{\sqrt{x^2+2mx+2018m+2019}}+\sqrt{mx^2+2mx+2020}\). Gọi S là tập hợp các giá trị nguyên của m để hàm số xác định trên R. Hỏi tập S có bao nhiêu phần tử?
Hàm số xác định khi \(\left\{{}\begin{matrix}x^2+2mx+2018m+2019>0\\mx^2+2mx+2020\ge0\end{matrix}\right.\)
Xét \(f\left(x\right)=x^2+2mx+2018m+2019\)
Có: \(\Delta'=m^2-2018m-2019\)
Để \(f\left(x\right)>0\) thì \(\Delta'< 0\Leftrightarrow m^2-2018m-2019< 0\Leftrightarrow-1< m< 2019\)(*)
Xét \(g\left(x\right)=mx^2+2mx+2020\)
Dễ thấy \(m=0\) thì \(g\left(x\right)=\sqrt{2020}>0\)(1)
Để \(g\left(x\right)\ge0\) thì \(\left\{{}\begin{matrix}m>0\\\Delta'\le0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m^2-2020m\le0\end{matrix}\right.\)\(\Leftrightarrow0< m\le2020\) (2)
(1),(2)\(\Rightarrow g\left(x\right)\ge0\Leftrightarrow0\le m\le2020\) (**)
(*),(**) suy ra hàm số xác định khi \(0\le m< 2019\)
Do đó tập hợp các giá trị nguyên của m để hàm số xác định là:
\(S=\left\{m\in Z|0\le m< 2019\right\}\) và tập hợp có 2019 phần tử
Cho hàm số y = f(x) xác định trên R và có đạo hàm y = f '(x) thỏa mãn f ' x = 1 − x x + 2 . g x + 2018 trong đó g x < 0 , ∀ x ∈ ℝ . Hàm số y = f 1 − x + 2018 x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞ .
B. (0;3)
C. − ∞ ; 3 .
D. 3 ; + ∞ .
Cho hàm số y = f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) = (1–x)(x+2)g(x)+2018 với g(x) < 0, ∀ x ∈ R . Hàm số y = f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞
B. 0 ; 3
C. - ∞ ; 3
D. 3 ; + ∞
Đáp án D
Ta có Đáp án D
Ta có y’ = –f’(1 – x) + 2018 = –[1–(1–x)][(1–x)+2]g(1–x) – 2018 + 2018
= –x(3–x)g(1–x)
Suy ra 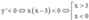 (vì g(1–x) < 0,
∀
x
∈
R
)
(vì g(1–x) < 0,
∀
x
∈
R
)
Vậy hàm số đã cho nghịch biến trên khoảng 3 ; + ∞
Tập xác định của hàm số y = 4 - 3 x - x 2 - 2019 là
A . ℝ \ { - 4 ; 1 }
B . ℝ
C . [ - 4 ; 1 ]
D . ( - 4 ; 1 )
Chọn A
Vì ![]() là hàm số lũy thừa có số mũ nguyên âm nên điều kiện xác định là
là hàm số lũy thừa có số mũ nguyên âm nên điều kiện xác định là 
Vậy tập xác định của hàm số là ![]()
Tập xác định của hàm số y = ( 4 - 3 x - x 2 ) - 2019 là
![]()
![]()
![]()
![]()
Tập xác định của hàm số y = 4 - 3 x - x 2 - 2019 là
A. R \ {-4; 1}
B. R
C. [-4; 1]
D. (-4; 1)
Cho hàm số y = f(x) xác định trên ℝ và có đạo hàm f '(x) thỏa mãn f ' x = 1 - x x + 2 . g x + 2018 trong đó g x < 0 , ∀ x ∈ ℝ . Hàm số y = f 1 - x + 2018 x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞
B. 0 ; 3
C. - ∞ ; 3
D. 3 ; + ∞
Đáp án D
Ta có y ' = f 1 - x + 2018 x + 2019 ' = 1 - x ' . f ' 1 - x + 2018 = - f ' 1 - x + 2018
= - x 3 - x . g 1 - x - 2018 + 2018 = - x 3 - x . g 1 - x mà g 1 - x < 0 ; ∀ x ∈ ℝ
Nên y ' < 0 ⇔ - x 3 - x . g 1 - x < 0 ⇔ x 3 - x . g 1 - x > 0 ⇔ x 3 - x < 0 ⇔ [ x > 3 x < 0
Khi đó, hàm số y = f 1 - x + 2018 x + 2019 nghịch biến trên khoảng 3 ; + ∞
Cho hàm số y=f(x) xác định trên R và có đạo hàm f‘(x) thỏa mãn f’(x)=(1-x)(x+2).g(x) + 2018 trong đó g(x)<0, mọi x thuộc R. Hàm số y=f(1-x)+2018x+2019 nghịch biến trên khoảng nào?
![]()
![]()
![]()
![]()
Tìm tập xác định D của hàm số y = l o g 2019 ( 4 - x 2 ) + ( 2 x - 3 ) - 2019 là
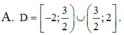
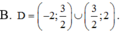
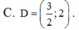
![]()