Cho hàm số y=x^3 +5x+7. Giá trị lớn nhất của hàm số trên đoạn [-5;0] bằng bao nhiêu?
A. 5
B. 7
C. 80
D. -143
Cho hàm số y = x 3 + 5 x + 7 . Giá trị lớn nhất của hàm số trên đoạn - 5 ; 0 bằng bao nhiêu?
A. 5
B. 7
C. 80
D. -143
Giá trị lớn nhất và nhỏ nhất của hàm số y = 5 x + 5 1 - x trên đoạn [0;1] là:
A. m i n 0 ; 1 y = 2 5 ; m a x 0 ; 1 y = 6
B. m i n 0 ; 1 y = 2 5 ; m a x 0 ; 1 y = 5
C. m i n 0 ; 1 y = 2 ; m a x 0 ; 1 y = 6
D. m i n 0 ; 1 y = 2 ; m a x 0 ; 1 y = 5
Chọn A.
Ta có: ![]() . Đặt
. Đặt ![]()
Khi đó ![]()
Hàm số f(t) xác định và liên tục trên đoạn [1 ;5]
Ta có: ![]() . Do đó
. Do đó ![]() .
.
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau

Biết rằng f(0)+f(3)=f(2)+f(5) Giá trị nhỏ nhất, giá trị lớn nhất của hàm số f(x) trên đoạn [0;5] lần lượt là
A. f(0), f(5)
B. f(2), f(0)
C. f(1), f(5)
D. f(2), f(5)
Dựa vào bảng xét dấu của f '(x) ta có bảng biến thiên của hàm số trên đoạn [0;5] như sau
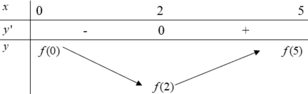
Suy ra ![]() Và
Và ![]()
Ta có ![]()
![]()
Vì f(x) đồng biến trên đoạn [2;5] nên ![]()
⇒ f(5)>f(0)
Vậy
![]()
Chọn đáp án D.
Cho hàm số y = x + 1 x - 1 . Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số trên đoạn [-5;-1]. Tính M + m
A. -6
B. 2 3
C. 3 2
D. 6 5
Đáp án B
Phương pháp:
Phương pháp tìm GTLN, GTNN của hàm số y = f(x) trên [a;b]
+) Bước 1: Tính y’, giải phương trình y' = 0 ⇒ xi ∈ [a;b]
+) Bước 2: Tính các giá trị f(a); f(b); f(xi)
+) Bước 3:


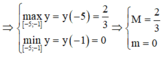
![]()
Cho hàm số y = x + 1 x - 1 . Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số trên đoạn [-5;-1]. Tính M+m
A. -6
B. 2 3
C. 3 2
D. 6 5
Cho hàm số f(x)=\(\left|x^4-4x^3+4x^2+a\right|\). Gọi M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn [0;2]. Có bao nhiêu số nguyên a thuộc đoạn [-3;3] sao cho M≤2m
A.3
B.7
C.6
D.5
\(g\left(x\right)=x^4-4x^3+4x^2+a\)
\(g'\left(x\right)=4x^3-12x^2+8x=0\Leftrightarrow4x\left(x^2-3x+2\right)\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=2\end{matrix}\right.\)
\(f\left(0\right)=f\left(2\right)=\left|a\right|\) ; \(f\left(1\right)=\left|a+1\right|\)
TH1: \(\left\{{}\begin{matrix}M=\left|a\right|\\m=\left|a+1\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|a\right|\ge\left|a+1\right|\\\left|a\right|\le2\left|a+1\right|\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}-\dfrac{2}{3}\le a\le-\dfrac{1}{2}\\a\le-2\end{matrix}\right.\) \(\Rightarrow a=\left\{-3;-2\right\}\)
TH2: \(\left\{{}\begin{matrix}M=\left|a+1\right|\\m=\left|a\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|a+1\right|\ge\left|a\right|\\\left|a+1\right|\le2\left|a\right|\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-\dfrac{1}{2}\le a\le-\dfrac{1}{3}\\a\ge1\end{matrix}\right.\) \(\Rightarrow a=\left\{1;2;3\right\}\)
Cho hàm số y=f(x) có bảng biến thiên như sau:
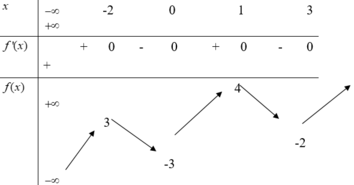
Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [-2;3] bằng
A. -6
B. -8
C. -12
D. -9
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 3 + x 2 - 5 x trên đoạn [0;2] lần lượt là
A. 1;0
B. 2; -3
C. 3; 1
D. 2; 1
Đáp án B
y ' = 3 x 2 + 2 x - 5 y ' = 0 ⇔ [ x = 1 x = - 5 3 y 0 = 0 , y 1 = - 3 , y 2 = 2
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 3 + x 2 − 5 x trên đoạn [0;2] lần lượt là:
A. 1;0
B. 2; -3
C. 3;1
D. 2;1