Tìm tung độ điểm cực đại (yCĐ) của ( C ) : y = x - 2 x 2 - 3
![]()
![]()

![]()
Tìm tung độ các điểm cực đại ( y C Đ ) và cực tiểu ( y C T ) của (C):
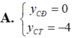
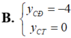
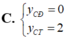
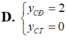
Cho (C): y = m x 4 - ( m 2 - 3 ) x 2 + m - 2 . Tìm m để (C) có 2 điểm cực tiểu và 1 điểm cực đại đồng thời y C Đ < 0
![]()
![]()
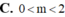
![]()
Tìm tung độ điểm cực đại y C N hoặc tung độ điểm cực tiểu Y C T nếu có của hàm số y = x 2 + 1 x + 2
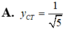
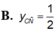
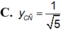
![]()
Tìm tung độ điểm cực đại củab ( C ) : y = x 2 - x + 1 x - 1
![]()
![]()
![]()
![]()
Tìm giá trị cực đại y C Đ của hàm số y = x 4 − 3 x 2 + 2 .
A. y C Đ = 2
B. y C Đ = − 2
C. y C Đ = − 1 4
D. y C Đ = 0
Đáp án A.
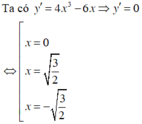
Dùng bảng biến thiên
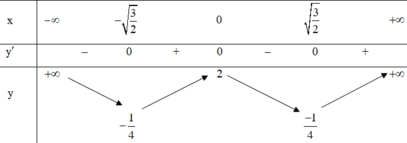
Hàm số đạt cực đại tại x = 0 nên y(0) = 2
Tìm y C D (tung độ điểm cực đại) và y C T (tung độ điểm cực tiểu) của đồ thị hàm số y = x 2 - 3 x + 3 x - 1
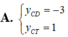
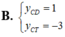

Tìm giá trị cực đại y C Đ của hàm số y = 4 1 + x 2 .
A. 3
B. 4
C. 2
D. 5
Tìm giá trị cực đại yCĐ của hàm số y = x 2 - 1 2
![]()
![]()
![]()
Tìm giá trị cực đại y C Đ của hàm số y = - x 4 + 2 x 2 - 5
A. -4
B. -5
C. -2
D. -6
Chọn A
![]()
Lập bảng biến thiên . Suy ra y C Đ = - 4