Đáp án A.
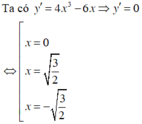
Dùng bảng biến thiên
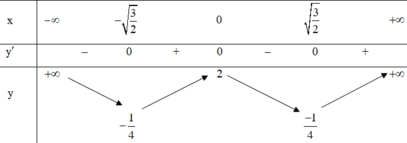
Hàm số đạt cực đại tại x = 0 nên y(0) = 2
Đáp án A.
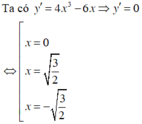
Dùng bảng biến thiên

Hàm số đạt cực đại tại x = 0 nên y(0) = 2
Cho hàm số y = a x 3 + b x 2 + c x + d đạt cực đại tại x = -2 với giá trị cực đại là 64; đạt cực tiểu tại x = 3 với giá trị cực tiểu là -61. Khi đó giá trị của a + b + c + d bằng
A. 1
B. 7
C. -17
D. 5
Cho hàm số y = f ( x ) = x 3 – ( 2 m - 1 ) x 2 + ( 2 - m ) x + 2 . Tập tất cả các giá trị của m để đồ thị hàm số y = f x có 5 điểm cực trị là a b ; c với a, b, c là các số nguyên và a b là phân số tối giản. Tính a+b+c
A. 11
B. 8
C. 10
D. 5
Cho a,b,c∈R sao cho hàm số y=x 3 + ax 2 + bx + c đạt cực trị tại x = 2 đồng thời có y(0)=1 và y(2)=-3. Hỏi trong không gian Oxyz, điểm M(a;b;c) nằm trong mặt cầu nào sau đây?
A. ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 16 .
B. ( x - 2 ) 2 + ( y - 3 ) 2 + ( z + 5 ) 2 = 64 .
C. x 2 + y 2 + ( z + 5 ) 2 = 36 .
D. ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 25 .
Xét tính đúng sai của các mệnh đề sau (với a, b, c, d là các hằng số).
(I): Giá trị cực đại của hàm số y = f x luôn lớn hơn giá trị cực tiểu của nó.
(II): Hàm số y = a 4 + b x + c a ≠ 0 luôn có ít nhất một cực trị
(III): Giá trị cực đại của hàm số y = f x luôn lớn hơn mọi giá trị của hàm số đó trên tập xác định.
(IV): Hàm số y = a x + b c x + d c ≠ 0 ; a d − b c ≠ 0 không có cực trị.
Số mệnh đề đúng là:
A. 1
B. 4
C. 3
D. 2
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a;b;c;d ∈ R, a ≠ 0) có đồ thị (C). Biết rằng đồ thị (C) đi qua gốc tọa độ và có đồ thị hàm số y = f’(x) cho bởi hình vẽ sau đây.

Tính giá trị H = f(4) – f(2)
A. H = 51
B. H = 54
C. H = 58
D. H = 64
Cho hàm số y = x + b a x − 2 có đồ thị là (C). Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của (C) tại điểm M 1 ; − 2 song song với đường thẳng 3 x + y − 4 = 0. Khi đó tổng giá trị của a + b bằng:
A. 2
B. 1
C. -1
D. 0
Hàm số y = a x 4 + b x 2 + c đạt cực đại tại A(0;-3) và đạt cực tiểu tại B(-1;-5). Khi đó, giá trị của a, b, c lần lượt là:
A. 2;4;-3
B. -3;-1;-5
C. -2;4;-3
D. 2;-4;-3
Cho hàm số y = f ( x ) liên tục trên ℝ và có đồ thị như hình vẽ bên. Xét 4 mệnh đề sau
(1) Hàm số y = f ( x ) đạt cực đại tại x 0 = 0
(2) Hàm số y = f ( x ) có ba cực trị.
(3) Phương trình y = f ( x ) có đúng ba nghiệm phân biệt
(4) Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]
Hỏi trong 4 mệnh đề trên, có bao nhiêu mệnh đề đúng?

A. 1
B. 3
C. 4
D. 2
Cho hàm số bậc ba y = ax 3 + bx 2 + cx + d có đồ thị nhận hai điểm A(0;3) và B(2;-1) làm hai điểm cực trị. Khi đó số điểm cực trị của hàm số y = | ax 2 | x | + bx 2 + c | x | + d | là
A. 5
B. 7
C. 9
D. 11
Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d , ( a , b , c , d ∈ ℝ ) thỏa mãn a > 0 , d > 0 > 2018 , a + b + c + d - 2018 < 0 Tìm số điểm cực trị của hàm số y = f ( x ) - 2018
A. 2
B. 1
C. 3
D. 5