Các câu hỏi tương tự
Tìm tung độ điểm cực đại (yCĐ) của
(
C
)
:
y
x
-
2
x
2
-
3
Đọc tiếp
Tìm tung độ điểm cực đại (yCĐ) của ( C ) : y = x - 2 x 2 - 3
![]()
![]()

![]()
Tìm
y
C
D
(tung độ điểm cực đại) và
y
C
T
(tung độ điểm cực tiểu) của đồ thị hàm số
y
x
2
-
3
x
+
3
x
-
1
Đọc tiếp
Tìm y C D (tung độ điểm cực đại) và y C T (tung độ điểm cực tiểu) của đồ thị hàm số y = x 2 - 3 x + 3 x - 1
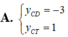
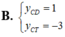

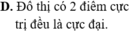
Tìm tung độ điểm cực đại
y
C
N
hoặc tung độ điểm cực tiểu
Y
C
T
nếu có của hàm số
y
x
2
+
1
x
+
2
Đọc tiếp
Tìm tung độ điểm cực đại y C N hoặc tung độ điểm cực tiểu Y C T nếu có của hàm số y = x 2 + 1 x + 2
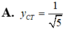
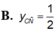
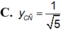
![]()
Tìm tung độ các điểm cực đại
(
y
C
D
)
và điểm cực tiểu
y
C
T
của đồ thị hàm số
y
x
2
x
-
1
Đọc tiếp
Tìm tung độ các điểm cực đại ( y C D ) và điểm cực tiểu y C T của đồ thị hàm số y = x 2 x - 1
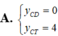
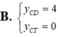
![]()
![]()
Biết đường thẳng (d): yx-1 là tiếp tuyến của (C):
y
x
-
1
2
x
-
1
. Tìm tung độ
y
M
của tiếp điểm.
Đọc tiếp
Biết đường thẳng (d): y=x-1 là tiếp tuyến của (C): y = x - 1 2 x - 1 . Tìm tung độ y M của tiếp điểm.
![]()
![]()
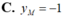
![]()
Tìm tung độ các điểm cực đại (
y
C
Đ
) và cực tiểu
(
y
C
T
)
của (C):
Đọc tiếp
Tìm tung độ các điểm cực đại ( y C Đ ) và cực tiểu ( y C T ) của (C):
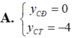
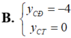
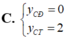
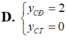
Tìm tất cả giá trị thực của m để hàm số y=x^4-2(m^2-m+1)x^2+m-1 có một điểm cực đại và hai điểm cực tiểu, đồng thời khoảng cách giữa hai điểm cực tiểu là ngắn nhất.
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
-
3
m
x
2
+
(
m
-
1
)
x
+
2
có cực đại, cực tiểu và các đ...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + ( m - 1 ) x + 2 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương
A. 0 ≤ m ≤ 1
B. m ≥ 1
C. m ≥ 0
D. m > 1
Tìm các giá trị của tham số m để đồ thị hàm số:
y
-
x
3
+
3
x
2
+
3
(
m
2
-
1
)
x
-...
Đọc tiếp
Tìm các giá trị của tham số m để đồ thị hàm số: y = - x 3 + 3 x 2 + 3 ( m 2 - 1 ) x - 3 m 2 - 1 có điểm cực đại và điểm cực tiểu cùng với gốc tọa độ tạo thành tam giác vuông tại O.
A. m = 1
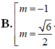
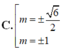
D. m = ± 1




