Cho hàm số y = f(x) xác định trên ℝ và có đồ thị như hình bên. Phương trình f x - 2 = - 1 2 có bao nhiêu nghiệm?
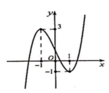
A. 2
B. 4
C. 5
D. 6
Chọn đáp án B
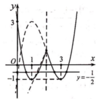
Đồ thị hàm số y = f(x – 2) là tịnh tiến đồ thị hàm số y = f(x) sang phải 2 đơn vị ta được đồ thị như hình bên.
Khi đó đồ thị hàm số f x - 2 được vẽ như sau:
- Giữ nguyên phần đồ thị bên phải đường thẳng x = 2.
- Bỏ phần đồ thị bên trái đường thẳng x = 2.
- Lấy đối xứng đường thẳng bên phải đường thẳng x = 2 qua đường thẳng x = 2.
Dựa vào đồ thị hàm số f x - 2 đường thẳng - 1 2 cắt đồ thị tại 4 điểm phân biệt khi đó phương trình f x - 2 = - 1 2 có 4 nghiệm phân biệt.
Cho hàm số y = f ( x ) xác định và liên tục trên ℝ . Đồ thị của hàm số f ( x ) như hình bên. Gọi m là số nghiệm thực của phương trình f ( f ( x ) ) = 1 . Khẳng định nào sau đây là đúng?
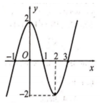
A. m = 5
B. m = 6
C. m = 7
D. m = 9
Cho hàm số y = f ( x ) xác định và liên tục trên ℝ . Đồ thị của hàm số f(x) như hình bên. Gọi m là số nghiệm thực của phương trình f(f(x))=1. Khẳng định nào sau đây là đúng?
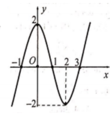
A. m=5
B. m=6
C. m=7
D. m=9
Cho hàm số y=f(x) có đạo hàm xác định trên tập ℝ / 0 và đồ thị hàm số y=f(x) như hình vẽ bên dưới. Có bao nhiêu giá trị nguyên của tham số m để phương trình f cos 2 x = m có nghiệm?
A. Không tồn tại m
B. 1
C. 2
D. 3
Cho hàm số y = f(x) xác định trên
ℝ
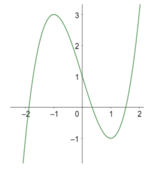
và có đồ thị hàm số y = f '(x) như hình vẽ bên.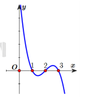
Xét các khẳng định sau:
(I) Hàm số y = f(x) có ba cực trị.
(II) Phương trình f(x) = m + 2018 có nhiều nhất ba nghiệm.
(III) Hàm số y = f(x + 1) nghịch biến trên khoảng (0;1) .
Số khẳng định đúng là:
A. 1
B. 3
C. 2
D. 0
Đáp án C
Ta có f ' x = 0 ⇔ x = 1 ; 2 ; 3 ⇒ hàm số có 3 điểm cực trị
Lại có g x = f x - m - 2018 ⇒ g ' x = f ' x = 0 ⇒ có 3 nghiệm phân biệt
Suy ra phương trình f x = m + 2018 có nhiều nhất 4 nghiệm
Xét y = f x + 1 ⇒ y ' = f ' x + 1 < 0 ⇔ [ x + 1 ∈ 1 ; 2 x + 1 ∈ 3 ; + ∞ ⇔ [ 0 < x < 1 x > 2
Suy ra hàm số y = f(x + 1) nghịch biến trên khoảng (0;1).
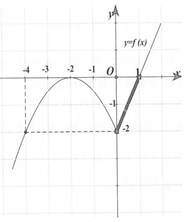
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình f(x) + m - 2018 = 0 có duy nhất một nghiệm.
A. m ≤ 2015, m ≥ 2019.
B. 2015 < m < 2019.
C. m = 2015, m = 2019.
D. m < 2015, m > 2019.
Chọn D
Phương pháp:
Biến đổi phương trình về f(x) = 2018 - m và sử dụng tương giao đồ thị: Phương trình có duy nhất một nghiệm khi và chỉ khi đường thẳng y = 2018 - m cắt đồ thị hàm số y = f(x) tại duy nhất một điểm.
Cách giải:
Phương trình f(x) + m - 2018 = 0 
Đây là phương trình hoành độ giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = 2018 - m (có phương song song hoặc trùng với trục hoành).
Dựa vào đồ thị, ta có ycbt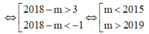 
Cho hàm số y=f(x) xác định và liên tục trên ℝ . Đồ thị của hàm số f(x) như hình bên. Số điểm cực trị của đồ thị hàm số y=f(f(x)) bằng?
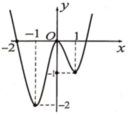
A. 8.
B. 9
C. 10.
D. 11.
Cho hàm số f(x) có đạo hàm f'(x) xác định, liên tục trên ℝ và có đồ thị f'(x) như hình vẽ bên. Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
Cho hàm số y= f(x) xác định trên R và có đồ thị như hình bên. Hỏi phương trình f(|x-2|) = -1/2 có bao nhiêu nghiệm?
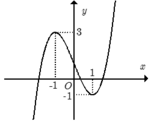
A. 2.
B. 0.
C. 6.
D. 4.
+ Trước tiên tịnh tiến đồ thị sang phải 2 đơn vị để được đồ thị hàm số y= f(x-2) .
Tiếp theo giữ phần đồ thị phía bên phải đường thẳng x= 2, xóa bỏ phần đồ thị phía bên trái đường thẳng x= 2.
Cuối cùng lấy đối xứng phần đồ thị vừa giữ lại ở trên qua đường thẳng x= 2. Ta được toàn bộ phần đồ thị của hàm số
y = f(|x-2|) (hĩnh vẽ bên dưới)
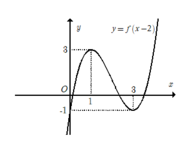
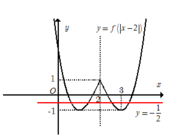
Dựa vào đồ thị hàm số y = f(|x -2|) , ta thấy đường thẳng y= -1/2 cắt đồ thị hàm số y = f(|x-2|) tại 4 điểm phân biệt khi và chỉ khi phương trình f(|x-2|) = -1/2 có 4 nghiệm phân biệt.
Chọn D.
