Cho hai tích phân ∫ - 2 5 f ( x ) d x = 8 và ∫ 5 - 2 g ( x ) d x = 3 . Tính I= ∫ - 2 5 f ( x ) - 4 g ( x ) - 1 d x ?
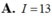
![]()
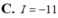
![]()
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) = 0, F(2) = 1, G(2) = 1 và ∫ 0 2 F ( x ) g ( x ) d x = 3 . Tính tích phân hàm: ∫ 0 2 G ( x ) f ( x ) d x
A. I = 3.
B. I = 0.
C. I = -2.
D. I = -4.
Chọn C.
Đặt u = G ( x ) d v = f ( x ) d x ⇒ d u = G ( x ) ' d x = g ( x ) d x v = ∫ f ( x ) d x = F ( x )
Suy ra: I = G ( x ) F ( x ) 2 0 - ∫ 0 2 F ( x ) g ( x ) d x
= G(2)F(2) – G(0)F(0) – 3 = 1 – 0 – 3 = -2.
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [1;4] thỏa mãn f(1)=-1, f(4)=-8 và x 3 ( f ' ( x ) ) 2 - f ( x ) = 9 x 3 - x - 3 x , ∀ x ∈ [ 1 ; 4 ] . Tích phân ∫ 1 4 f ( x ) d x bằng
A. -7
B. - 89 6
C. - 79 6
D. -8
Cho hàm f(x) liên tục trên R và ∫ 0 1 x . f ( x ) d x = 5 Tích phân - 1 4 ∫ 0 π 4 f ( cos 2 x ) d ( cos 4 x ) bằng
![]()
![]()
![]()
![]()
Cho hàm số y = f(x) thỏa mãn ∫ 0 1 f ( x ) d x = 2 v à ∫ 1 5 f ( x ) d x = - 8 . Tính tích phân I = ∫ - 1 2 f 2 x - 3 d x .
A. I = -8
B. I = -2
C. I = -4
D. I = -6
Cho hàm số y=f(x) thỏa mãn ∫ 0 1 f ( x ) d x = 2 và ∫ 1 5 f ( x ) d x = - 8 . Tính tích phân I = ∫ - 1 2 f 2 x - 3 d x
![]()
![]()
![]()
![]()
X, Y là hai este đều đơn chức và là đồng phân của nhau. Hóa hơi hoàn toàn 11,0 gam X thì thể tích hơi đúng bằng thể tích của 3,5 gam N2 (đo cùng điều kiện). Thủy phân hoàn toàn hỗn hợp E chứa X, Y trong môi trường axit, thu được một axit cacboxylic Z duy nhất và hỗn hợp F chứa 2 ancol. Cho các phát biểu sau:
(a) X, Y, Z đều cho phản ứng tráng gương.
(b) Phân tử X và Y hơn kém nhau một nhóm metyl.
(c) Đun F với H2SO4 đặc ở 1700C thu được 2 anken.
(d) Hai ancol trong F là đồng phân cấu tạo của nhau.
Số phát biểu đúng là:
A. 1
B. 2
C. 3
D. 4
Phân tích các đa thức sau thành nhân tử:
a) \({\left( {x - 1} \right)^2} - 4\)
b) \(4{x^2} + 12x + 9\)
c) \({x^3} - 8{y^6}\)
d) \({x^5} - {x^3} - {x^2} + 1\)
e) \( - 4{x^3} + 4{x^2} + x - 1\)
f) \(8{x^3} + 12{x^2} + 6x + 1\)
\(a,\left(x-1\right)^2-2^2=\left(x-1-2\right)\left(x-1+2\right)=\left(x-3\right)\left(x+1\right)\\ b,=\left(2x\right)^2+2.2x.3+3^2\\ =\left(2x+3\right)^2\\ c,=x^3-\left(2y\right)^3\\ =\left(x-2y\right)\left(x^2+2xy+4y^2\right)\\ d,=x^3\left(x^2-1\right)-\left(x^2-1\right)\\ =\left(x^3-1\right)\left(x^2-1\right)\\ =\left(x-1\right)\left(x^2+x+1\right)\left(x-1\right)\left(x+1\right)\\ =\left(x-1\right)\left(x+1\right)\left(x^2+x+1\right)\)
\(e,=-4x^2\left(x-1\right)+\left(x-1\right)\\ =\left(1-4x^2\right)\left(x-1\right)\\ =\left(1-2x\right)\left(1+2x\right)\left(x-1\right)\)
\(f,=\left(2x\right)^3+3.\left(2x\right)^2.1+3.2x.1^2+1^3\\ =\left(2x+1\right)^3\)
Biết F(x) là nguyên hàm của f(x) trên R thỏa mãn ∫ 1 e F ( x ) d ( ln x ) = 3 và F ( e ) = 5 Tích phân ∫ 1 e ln x . f ( x ) d x bằng
![]()
![]()
![]()
![]()
Cho hàm số f (x) có đạo hàm cấp hai liên tục trên đoạn [0;1] thoả mãn [ f ' ( x ) ] 2 + f ( x ) f '' ( x ) ≥ 1 , ∀ x ∈ [ 0 ; 1 ] và f 2 ( 0 ) + f ( 0 ) . f ' ( 0 ) = 3 2 . Giá trị nhỏ nhất của tích phân ∫ 0 1 f 2 ( x ) d x bằng
A. 5 2
B. 1 2
C. 11 6
D. 7 2