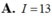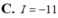Các câu hỏi tương tự
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) 0, F(2) 1, G(2) 1 và
∫
0
2
F
(
x
)
g
(
x
)
d
x
3 . Tính tích phân hàm:
∫
0
2
G
(
x
)
f
(
x
)
d
x
A. I 3. B. I 0....
Đọc tiếp
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) = 0, F(2) = 1, G(2) = 1 và ∫ 0 2 F ( x ) g ( x ) d x = 3 . Tính tích phân hàm: ∫ 0 2 G ( x ) f ( x ) d x
A. I = 3.
B. I = 0.
C. I = -2.
D. I = -4.
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Cho hàm số f(x) thỏa mãn
∫
1
2
(
2
x
+
3
)
.
f
(
x
)
d
x
15
và
7
.
f
(
2
)
-
5
.
f
(
1
)
8
Tính I
∫
1
2
f
(...
Đọc tiếp
Cho hàm số f(x) thỏa mãn ∫ 1 2 ( 2 x + 3 ) . f ' ( x ) d x = 15 và 7 . f ( 2 ) - 5 . f ( 1 ) = 8 Tính I= ∫ 1 2 f ( x ) d x .
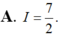
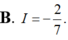

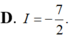
Cho hàm số y f(x) liên tục trên R và hàm số
y
g
(
x
)
x
f
(
x
2
)
có đồ thị trên đoạn [1;2] như hình vẽ bên. Biết phần diện tích miền được tô màu là S 5/2 , tính tích phân
I
∫
1
4
f
(
x
)
d
x...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và hàm số y = g ( x ) = x f ( x 2 ) có đồ thị trên đoạn [1;2] như hình vẽ bên. Biết phần diện tích miền được tô màu là S = 5/2 , tính tích phân I = ∫ 1 4 f ( x ) d x
A. I = 7
B. I = 6
C. I = 10
D. I = 5
Cho hàm số y f(x) liên tục trên R và hàm số y g(x) x.f(x2) có đồ thị trên đoạn [0;2] như hình vẽ bên. Biết diện tích S của miền được tô đậm bằng 5/2 tính tích phân
I
∫
1
4
f
(
x
)
d
x
A. I 5/4 B. I 5/2 C. I 5 D. I 10
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và hàm số y = g(x) = x.f(x2) có đồ thị trên đoạn [0;2] như hình vẽ bên. Biết diện tích S của miền được tô đậm bằng 5/2 tính tích phân I = ∫ 1 4 f ( x ) d x
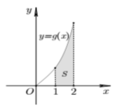
A. I = 5/4
B. I = 5/2
C. I = 5
D. I = 10
Biết F(x) là nguyên hàm của f(x) trên R thỏa mãn
∫
1
e
F
(
x
)
d
(
ln
x
)
3
và
F
(
e
)
5
Tích phân
∫
1
e
ln
x
.
f
(
x
)
d
x
bằng
Đọc tiếp
Biết F(x) là nguyên hàm của f(x) trên R thỏa mãn ∫ 1 e F ( x ) d ( ln x ) = 3 và F ( e ) = 5 Tích phân ∫ 1 e ln x . f ( x ) d x bằng
![]()
![]()
![]()
![]()
Cho hàm số y f( x) có đạo hàm
f
(
x
)
x
2
(
x
-
9
)
(
x
-
4
)
2
.
Xét hàm số y g( x) f( x2) Trong các phát biểu sau; tìm số phát biểu đúng I. Hàm số y g( x) đồng biến trên( 3; +∞) II. Hàm số y g(x) nghịch biến trê...
Đọc tiếp
Cho hàm số y= f( x) có đạo hàm f ' ( x ) = x 2 ( x - 9 ) ( x - 4 ) 2 . Xét hàm số y= g( x) =f( x2) Trong các phát biểu sau; tìm số phát biểu đúng
I. Hàm số y = g( x) đồng biến trên( 3; +∞)
II. Hàm số y= g(x) nghịch biến trên( -∞; -3)
III. Hàm số y= g( x) có 5 điểm cực trị
IV. m i n x ∈ R g ( x ) = f ( 9 )
A. 1
B. 2
C. 3
D. 4
Cho hàm số f(x) và g(x) có đạo hàm trên [1;4] và thỏa mãn hệ thức sau với mọi
x
∈
[1;4] f(1)2g(1)2; f(x)
1
x
x
.
1
g
(
x
)
; g(x)
-
2
x
x
....
Đọc tiếp
Cho hàm số f(x) và g(x) có đạo hàm trên [1;4] và thỏa mãn hệ thức sau với mọi x ∈ [1;4]
f(1)=2g(1)=2; f'(x)= 1 x x . 1 g ( x ) ; g(x)= - 2 x x . 1 f ( x ) . Tính I= ∫ 1 4 [ f ( x ) . g ( x ) ] d x
![]()
![]()
![]()
![]()
Biết F(x) là nguyên hàm của f(x) trên R thỏa mãn
∫
1
e
F
(
x
)
d
(
ln
x
)
3
và F(e)5 Tính
I
∫
1
e
ln
x
.
f
(
x
)
d
x
A. I 3 B. I –3 C. I 2 D. I –2
Đọc tiếp
Biết F(x) là nguyên hàm của f(x) trên R thỏa mãn ∫ 1 e F ( x ) d ( ln x ) = 3 và F(e)=5 Tính I = ∫ 1 e ln x . f ( x ) d x
A. I = 3
B. I = –3
C. I = 2
D. I = –2
Cho hàm số yf(x) liên tục trên R và thỏa mãn f(x) + f(
π
3
-
x
)
1
2
sin
x
cos
x
(
8
cos
3
x
+
1
)
,
∀
x
∈...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và thỏa mãn f(x) + f( π 3 - x )= 1 2 sin x cos x ( 8 cos 3 x + 1 ) , ∀ x ∈ R Biết tích phân I= ∫ 0 π 3 f ( x ) d x được biểu diễn dưới dạng I= a b ln c d ; a , b , c , d ∈ Z và các phân số a b ; c d là các phân số tối giản. Tính S= a 3 + a b - c + d
![]()
![]()
![]()
![]()