Tiếp tuyến của đồ thị hàm số y = f x = x x + 1 x + 2 . . . x + 2019 tại điểm có hoành độ x = 0 là
A. y = - 2019 ! x
B. y = x 2019 !
C. y = - x 2019 !
D. y = 2019 ! x
Những câu hỏi liên quan
Cho hàm số yf(x) có đạo hàm liên tục trên tập R/
2
và có đồ thị hàm số yf’(x) như hình vẽ. Biết
f
1
≠
10
f(3)4 . Có bao nhiêu tiếp tuyến của đồ thị hàm số mà tiếp tuyến đó song song với đường thẳng 3x+y-13 A. 2 B. 1 C. 0. D. 3
Đọc tiếp
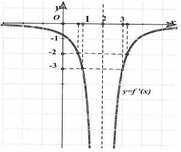
Cho hàm số y=f(x) có đạo hàm liên tục trên tập R/ 2 và có đồ thị hàm số y=f’(x) như hình vẽ. Biết f 1 ≠ 10 f(3)=4 . Có bao nhiêu tiếp tuyến của đồ thị hàm số mà tiếp tuyến đó song song với đường thẳng 3x+y-13
A. 2
B. 1
C. 0.
D. 3
Cho hàm số yf(x) có đạo hàm f’(x) trên R thỏa mãn
f
2
1
+
2
x
x
−
f
3
1
−
x
. Tiếp tuyến của đồ thị hàm số yf(x) tại điểm có hoành độ x1 là A.
y
−
1
7
x
−...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f’(x) trên R thỏa mãn f 2 1 + 2 x = x − f 3 1 − x . Tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x=1 là
A. y = − 1 7 x − 6 7 .
B. y = 1 7 x − 8 7 .
C. y = - 1 7 x + 8 7 .
D. y = − x + 6 7 .
Cho hàm số y f(x)
a
x
+
b
c
x
+
d
( a,b,c,d
∈
ℝ
,
-
d
c
≠
0) đồ thị hàm số y f’(x) như hình vẽ. Biết đồ thị hàm số y f(x) cắt...
Đọc tiếp
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.
Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
+ Ta có y ' = f ' ( x ) = a d - b c ( c x + d ) 2 . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
⇒ a d - b c ( 2 c + d ) 2 = 2 ↔ a d - b c = 2 ( 2 c + d ) 2
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
⇒ a d - b c d 2 = 2 ↔ a d - b c = 2 d 2
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
⇒ y = x - 3 x - 1
Chọn D.
Đúng 0
Bình luận (0)
Tiếp tuyến của đồ thị hàm số y = f ( x ) = x 4 có hệ số góc của tiếp tuyến là -4 có phương trình là:
A. y= -4x+5
B. y= =4x-3
C. y= -4x-4
D. y= -4x-5
cho đồ thị hàm số y=f(x),y=g(x) cùng tiếp xúc với đường thẳng (d):2x-y+1=0 tại M(1,3). Lập phương trình tiếp tuyến với đồ thị hàm số h(x)=f(x)*g(x)+2021x tại điểm có hoành độ bằng 1
Cho hàm số yf(x) có đạo hàm f (x) trên R thỏa mãn
f
2
1
+
2
x
x
−
f
3
1
−
x
. Tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x1 là A.
y
−
1
7
x
−...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f '(x) trên R thỏa mãn f 2 1 + 2 x = x − f 3 1 − x . Tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x=1 là
A. y = − 1 7 x − 6 7 .
B. y = 1 7 x − 8 7 .
C. y = − 1 7 x + 8 7 .
D. y = − x + 6 7 .
Đáp án A
Với x=0 thay vào hai vế của đẳng thức f 2 1 + 2 x = x − f 3 1 − x ta có f 2 1 = − f 3 1 .
Đạo hàm hai vế của đẳng thức đã cho, ta có:
4 f 1 + 2 x . f ' 1 + 2 x = 1 + 3 f 2 1 − x . f ' 1 − x → x = 0 2 f 1 . f ' 1 = 1 + 3 f 2 1 . f ' 1
Ta có hệ phương trình sau: f 2 1 = − f 3 1 4 f 1 . f ' 1 = 1 + 3 f 2 1 . f ' 1
⇔ f 2 1 f 1 + 1 = 0 4 f 1 . f ' 1 = 1 + 3 f 2 1 . f ' 1 ⇔ f 1 = − 1 f ' 1 = − 1 7
Vậy tiếp tuyến cần tìm là
y
=
f
'
1
.
x
−
1
+
f
1
=
−
1
7
x
−
1
−
1
⇔
y
=
−
1
7
x
−
6
7
Đúng 0
Bình luận (0)
Cho hàm số y=f(x)=-x3+x2-1 có đồ thị (C):
Viết phương trình tiếp tuyến với đồ thị của hàm số tại điểm có hoành độ bằng 2
f'(x)=y'=-3x^2+2x
f'(2)=-3*2^2+2*2=-3*4+4=-8
f(2)=-2^3+2^2-1=-8-1+4=-9+4=-5
y=f(2)+f'(2)(x-2)
=-5+(-8)(x-2)
=-8x+16-5
=-8x+11
Đúng 1
Bình luận (0)
Cho hàm số yf(x) có đạo hàm liên tục trên (
0
;
+
∞
) thỏa mãn
f
(
x
)
+
f
(
x
)
x
4
x
2
+
3
x
và f(1)2. Phương trình tiếp tuyến của đồ thị hàm số yf(x) tại điểm có hoành độ x 2 là x A. y 16x+20. B. y -16x+20 C. y...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên ( 0 ; + ∞ ) thỏa mãn f ' ( x ) + f ( x ) x = 4 x 2 + 3 x và f(1)=2. Phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x = 2 là x
A. y = 16x+20.
B. y = -16x+20
C. y = -16x-20
D. y = 16x-20.
Nếu hàm số yf(x) có đạo hàm tại xo thì phương trình tiếp tuyến của đồ thị hàm số tại điểm M(x0;f(x0)) là
Đọc tiếp
Nếu hàm số y=f(x) có đạo hàm tại xo thì phương trình tiếp tuyến của đồ thị hàm số tại điểm M(x0;f(x0)) là
Cho hàm số
y
f
(
x
)
xác định. Có đạo hàm trên R thỏa mãn:
f
-
x
+
2
2
+
f
x
+
2...
Đọc tiếp
Cho hàm số y = f ( x ) xác định. Có đạo hàm trên R thỏa mãn: f - x + 2 2 + f x + 2 3 = 10 x Viết phương trình tiếp tuyến của đồ thị hàm số y = f ( x ) tại điểm có hoành độ bằng 2
A. y=2x-5
B. y=2x-3
C. y=-2x+5
D. y=-2x+3
