Một vật dao động điều hoà dọc theo phương trình: x = 5 cos 2 π t 3 - π 3 ( c m ) . Kể từ thời điểm t = 0, sau thời gian bao lâu thì vật đi được quãng đường 7,5 cm?
A. 1,25 s
B. 1,5 s
C. 0,5 s
D. 0,25 s
Một con lắc lò xo dao động điều hoà theo phương trình dao động x=4 cos(0,5πt-π/3), thời điểm vật đi qua vị trí x=-2 cm theo chiều âm lần thứ 2012 kể từ khi vật bắt đầu dao động là
A.8043,3s B.4023,3s C.8046s 4026s
Một vật dao động điều hoà dọc theo trục Ox với phương trình: x = 10cos(πt - π/6 ) cm. Quãng đường vật đi được từ thời điểm t1 = 0,5s đến thời điểm t2 = 1s
A. 17,3cm
B. 13,7 cm
C. 3,66cm
D. 6,34 cm
Một vật dao động điều hòa dọc theo trục Ox với phương trình dao động là x = 4 cos ( 2 πt - π / 3 ) cm (t tính bằng s). Lấy π 2 = 10 . Gia tốc của vật khi có li độ bằng 3 cm là
A. ‒12 cm/s2
B. 120 cm/s2
C. ‒1,2 cm/s2
D. ‒60 cm/s2
Một vật dao động điều hòa dọc theo trục Ox với phương trình vận tốc là overline v = 16π cos(4πt - π/6) cm/ s . Xác định thời điểm lần thứ 2023 vật chuyển động nhanh dần qua vị trí x =2 kể từ lúc bắt đầu dao động
Từ pt \(v=16\pi\cos\left(4\pi t-\dfrac{\pi}{6}\right)=16\pi\cos\left(4\pi t-\dfrac{2\pi}{3}+\dfrac{\pi}{2}\right)\) (cm/s), ta suy ra \(\omega=4\pi\left(rad/s\right)\), lại có \(\omega A=16\pi\Leftrightarrow A=\dfrac{16\pi}{\omega}=4\left(cm\right)\)
\(\varphi_0=-\dfrac{2\pi}{3}\); \(T=\dfrac{2\pi}{\omega}=0,5\left(s\right)\)
Đường tròn lượng giác:
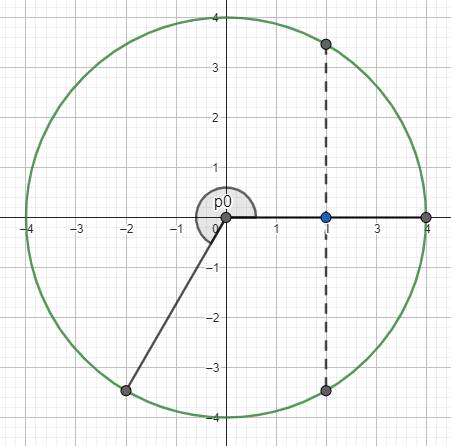
Từ đây, ta có thể thấy tại thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ khi dao động, góc quét của vật là \(\Delta\varphi=\dfrac{\pi}{3}+1011.2\pi=\dfrac{6067}{3}\pi\) (rad)
Thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ lúc bắt đầu dao động là \(\Delta t=\dfrac{\Delta\varphi}{2\pi}.T=\dfrac{\dfrac{6067}{3}\pi}{2\pi}.0,5=\dfrac{6067}{12}\approx505,58\left(s\right)\)
Một vật dao động điều hoà dọc theo trục Ox với phương trình : x = 10cos(πt - π/6 )cm. Quãng đường vật đi được từ thời điểm t1 = 0,5 s đến thời điểm t2 = 1 s
A. 17,3cm.
B. 13,7 cm.
C. 3,66cm.
D. 6,34 cm
Đáp án B
Phương pháp: Sử dụng đường tròn lượng giác
Cách giải:
Chu kỳ dao động T = 2s
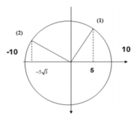
Quan sát trên hình vẽ ta thấy quãng đường vật đi được từ thời điểm t1 = 0,5s ứng với vị trí (1) đến thời điểm t2 = 1s ứng với vị trí (2) là: (5 + 5 3 ) = 13,7cm
Một vật dao động điều hoà xung quang vị trí cân bằng, dọc theo trục x' ox cod li độ thoả mãn phương trình : x = 10 cos( 4pi t + pi/4) (cm). Tìm biên độ, chu kì, pha ban đầu của dao động.
. Một vật dao động điều hoà dọc theo trục Ox. Lúc vật qua vị trí có li độ x = -√2 cm thì có vận tốc v = -π√2 cm/s và gia tốc a = π2√2 cm/s2. Chọn gốc toạ độ ở vị trí trên. Phương trình dao động của vật dưới dạng hàm số sin.
Một vật dao động điều hoà theo phương trình x = 4cos(5πt – π/3) cm. Biên độ dao động và pha ban đầu của vật là
A. 4 cm và 2π/3 rad
B. 4 cm và 4π/3 rad
C. 4 cm và - π/3 rad
D. 4 cm và π/3 rad
Chọn C.
Vật dao động điều hoà theo phương trình x = 4cos(5πt – π/3) cm có biên độ A = 4cm và pha ban đầu φ = – π/3 rad
Một vật nhỏ dao động điều hòa dọc theo trục Ox có phương trình dao động là x = 12cos(2πt + π/3) cm. Biên độ dao động của vật là
A. 6 cm
B. 6 2 cm
C. 3 cm
D. 12 cm
Biên độ dao động của vật A = 12cm
Đáp án D
Một vật nhỏ dao động điều hòa dọc theo trục Ox có phương trình dao động là x = 12cos(2πt + π/3) cm. Biên độ dao động của vật là
A. 2π cm.
B. 6 cm.
C. π/3 cm.
D. 12 cm
Đáp án D
+ Biên độ dao động của vật A=12cm