Tìm tung độ điểm cực đại củab ( C ) : y = x 2 - x + 1 x - 1
![]()
![]()
![]()
![]()
Tìm tung độ điểm cực đại (yCĐ) của ( C ) : y = x - 2 x 2 - 3
![]()
![]()

![]()
Tìm tung độ điểm cực đại y C N hoặc tung độ điểm cực tiểu Y C T nếu có của hàm số y = x 2 + 1 x + 2
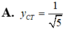
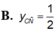
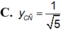
![]()
Tìm y C D (tung độ điểm cực đại) và y C T (tung độ điểm cực tiểu) của đồ thị hàm số y = x 2 - 3 x + 3 x - 1
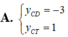
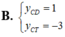

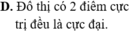
Tìm tung độ các điểm cực đại ( y C D ) và điểm cực tiểu y C T của đồ thị hàm số y = x 2 x - 1
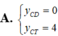
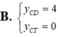
![]()
![]()
Tìm tung độ các điểm cực đại ( y C Đ ) và cực tiểu ( y C T ) của (C):
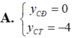
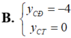
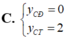
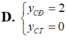
tìm parabol y= ax^2 +bx+c biết rằng parabol đó:
a/ đi qua 3 điểm A (-1;2) ; B( 2;0) ; C( 3;1)
b/ có đỉnh S ( 2;-1) và cắt trục tung tại điểm có tung độ bằng -3
c/ đạt cực đại tại I (1;3) và đi qua gốc tọa độ
d/ đạt cực tiểu bằng 4 tại x= -2 và đi qua B(0;6)
e/ cắt ox tại 2 điểm có hoành độ là -1 và 2, cắt oy tại điểm có tung độ bằng -2
tìm giá trị của m để đồ thị của hàm số y=x3+x2+(m+2)x
1. có cực đại và cực tiểu
2. có 2 điểm cực trị nằm về 2 phía của trục tung
3. có 2 điểm cực trị với hoành độ âm
4. đạt cực tiểu tại x=2
Lời giải:
1.
Để ĐTHS có cực đại và cực tiểu thì \(y'=3x^2+2x+m+2=0\) có hai nghiệm phân biệt
\(\Leftrightarrow \Delta'=1-3(m+2)>0\Leftrightarrow m<\frac{-5}{3}\)
2.
ĐTHS có hai cực trị nằm về hai phía trục tung nghĩa là PT \(y'=3x^2+2x+m+2=0\) có hai nghiệm $x_1,x_2$ trái dấu.
Theo định lý Viete thì \(x_1x_2=\frac{m+2}{3}<0\Leftrightarrow m<-2\)
3. Áp dụng định lý Viete:
Cực trị với hoành độ âm thì: \(\left\{\begin{matrix} x_1+x_2=\frac{-2}{3}<0\\ x_1x_2=\frac{m+2}{3}>0\end{matrix}\right.\Leftrightarrow m>-2\Rightarrow -2< m<\frac{-5}{3}\)
4. Để ĐTHS có cực tiểu tại $x=2$ thì PT \(y'=3x^2+2x+m+2=0\) nhận $x=2$ là nghiệm \(\Leftrightarrow m=-18\)
Thử lại bằng bảng biến thiên ta thấy đúng.
Tìm tung độ điểm cực tiểu của (C): y = 3 x 2 3 - 2 x
![]()
![]()
![]()
![]()
Xác định m để đồ thị hàm số y= -x3 + 3x2 -(m2 -3m+2)x -4 có các điểm cực đại và cực tiểu nằm về 2 phía của trục tung