Họ nguyên hàm của hàm số f(x) = 4x(1+ln x) là
A. 2 x 2 ln x + 3 x 2
B. 2 x 2 ln x + x 2
C. 2 x 2 ln x + 3 x 2 + C
D. 2 x 2 ln x + x 2 + C
Họ nguyên hàm của hàm số f(x) = 2x ( 2 + ln x) là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Họ các nguyên hàm của hàm số f(x) = (2x + 1) ln x là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
4. Tính đạo hàm của các hàm số sau:
a) \(y = (3x^2-4x+1)^{-4}\)
b) \(y = 3^{x^2-1} + e^{-x+1}\)
c) \(y = \ln (x^2-4x) + \log_{3} (2x-1)\)
d) \(y =x . \ln x + 2^{\frac{x-1}{x+1}}\)
e) \(y = x^{-7} - \ln (x^2-1)\)
`a)TXĐ:R\\{1;1/3}`
`y'=[-4(6x-4)]/[(3x^2-4x+1)^5]`
`b)TXĐ:R`
`y'=2x. 3^[x^2-1] ln 3-e^[-x+1]`
`c)TXĐ: (4;+oo)`
`y'=[2x-4]/[x^2-4x]+2/[(2x-1).ln 3]`
`d)TXĐ:(0;+oo)`
`y'=ln x+2/[(x+1)^2].2^[[x-1]/[x+1]].ln 2`
`e)TXĐ:(-oo;-1)uu(1;+oo)`
`y'=-7x^[-8]-[2x]/[x^2-1]`
Lời giải:
a.
$y'=-4(3x^2-4x+1)^{-5}(3x^2-4x+1)'$
$=-4(3x^2-4x+1)^{-5}(6x-4)$
$=-8(3x-2)(3x^2-4x+1)^{-5}$
b.
$y'=(3^{x^2-1})'+(e^{-x+1})'$
$=(x^2-1)'3^{x^2-1}\ln 3 + (-x+1)'e^{-x+1}$
$=2x.3^{x^2-1}.\ln 3 -e^{-x+1}$
c.
$y'=\frac{(x^2-4x)'}{x^2-4x}+\frac{(2x-1)'}{(2x-1)\ln 3}$
$=\frac{2x-4}{x^2-4x}+\frac{2}{(2x-1)\ln 3}$
d.
\(y'=(x\ln x)'+(2^{\frac{x-1}{x+1}})'=x(\ln x)'+x'\ln x+(\frac{x-1}{x+1})'.2^{\frac{x-1}{x+1}}\ln 2\)
\(=x.\frac{1}{x}+\ln x+\frac{2}{(x+1)^2}.2^{\frac{x-1}{x+1}}\ln 2\\ =1+\ln x+\frac{2^{\frac{2x}{x+1}}\ln 2}{(x+1)^2}\)
e.
\(y'=-7x^{-8}-\frac{(x^2-1)'}{x^2-1}=-7x^{-8}-\frac{2x}{x^2-1}\)
Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số f x = 1 1 + sinx
a) F(x) = 1 - cos x 2 + π 4
b) G(x) = 2 tan x 2
c) H(x) = ln(1 + sinx)
d) K(x) = 2 1 - 1 1 + tan x 2
a) F(x) = 1 - cos x 2 + π 4
d) K(x) = 2 1 - 1 1 + tan x 2
Hàm số F(x) = ln|sin x – cos x| là một nguyên hàm của hàm số
A. f ( x ) = sin x + cos x sin x - cos x
B. f ( x ) = sin x - cos x sin x + cos x
C. f ( x ) = 1 sin x + cos x
D. f ( x ) = 1 sin x - cos x
Chọn A.
F ' ( x ) = sin x - cos x ' sin x - cos x = cos x + sin x sin x - cos x
Cho F(x) là một nguyên hàm của hàm số f(x)=x ln x Tính F ' ' x
A. F ' ' x = 1 − ln x
B. F ' ' x = 1 x
C. F ' ' x = 1 + ln x
D. F ' ' x = x + ln x
Đáp án C
Ta có F ' ' x = f ' x = 1 + ln x
Kí hiệu F (x) là một nguyên hàm của hàm số f ( x ) = 1 e x + 1 , biết F 0 = - ln 2 . Tìm tập nghiệm S của phương trình F ( x ) + ln ( e x + 1 ) = 3 .
A. S = - 3 ; 3
B. S = 3
C. S = ∅
D. S = - 3
Đáp án B
∫ 1 e x + 1 d x = ∫ d x - ∫ e x e x + 1 d x = x - ln ( e x + 1 ) + C
Vì F ( 0 ) = = - ln 2 ⇔ C = 0 ⇒ F ( x ) = x - ln e x + 1
Xét phương trình F ( x ) + ln ( e x + 1 ) = 3 ⇔ x = 3
Giả sử F(x) là một nguyên hàm của f ( x ) = ln ( x + 3 ) x 2 sao cho F(-2)+F(1)=0. Giá trị của F(-1)+F(2) bằng
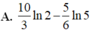
B. 0
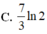
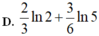
Cho F(x) là một nguyên hàm của hàm số 1 e x + 1 , thỏa mãn F ( 0 ) = - ln 2 . Tìm tập nghiệm S của phương trình F ( x ) + l n ( e x + 1 ) = 3
A. S = 3
B. S = - 3
C. S = ∅
D. S = ± 3