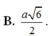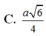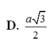Cho hình chóp S.ABCD đáy là hình thang cân có A B = C D = B C = a , A D = 2 . Cạnh bên SA vuông góc với đáy, SA = 2a. Thể tích khối cầu ngoại tiếp hình chóp S.BCD là:
A. 8 2 π a 3 3
B. 16 2 π a 3 3
C. 16 π a 3 3
D. 32 2 π a 3 3
Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB a, cạnh đáy CD 2a, AD a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng
3
a
2
2
. Thể tích của hình chóp S.ABCD bằng:A.
a
3
B.
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB = a, cạnh đáy CD = 2a, AD = a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng 3 a 2 2 . Thể tích của hình chóp S.ABCD bằng:
A. a 3 B. 3 a 3 2
C. 3 a 3 D. 3 2 a 3
Chọn A.
Gọi H là trung điểm của CD, M là trung điểm của BC. Khi đó HM ⊥ BC, SM ⊥ BC. Dễ thấy tam giác HBC vuông cân ở H, do đó tính được BC, SM. Từ đó tính được SH.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình thang cân,
S
A
⊥
A
B
C
D
,
A
D
2
B
C
2
A
B
. Trong tất cả các tam giác mà 3 đỉnh lấy từ 5 điểm S, A, B, C, D có bao nhiêu tam giác vuông? A. 3 B. 6 C. 5 D. 7
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang cân, S A ⊥ A B C D , A D = 2 B C = 2 A B . Trong tất cả các tam giác mà 3 đỉnh lấy từ 5 điểm S, A, B, C, D có bao nhiêu tam giác vuông?
A. 3
B. 6
C. 5
D. 7
Cho hình chóp S.ABCD có đáy là hình thang cân,
S
A
⊥
A
B
C
D
,
A
D
2
B
C
2
A
B
. Trong tất cả các tam giác mà 3 đỉnh lấy từ 5 điểm S, A, B, C, D có bao nhiêu tam giác vuông? A. 3 B. 6 C. 5 D. 7
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang cân, S A ⊥ A B C D , A D = 2 B C = 2 A B . Trong tất cả các tam giác mà 3 đỉnh lấy từ 5 điểm S, A, B, C, D có bao nhiêu tam giác vuông?
A. 3
B. 6
C. 5
D. 7
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đặt
S
A
→
a
→
,
S
B
→
b
→
,
S
C
→
c
→
,
S
D
→
d
→
....
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đặt S A → = a → , S B → = b → , S C → = c → , S D → = d → . Chứng minh: a → + c → = d → + b → .
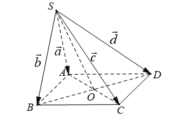
- Gọi O là tâm của hình bình hành ABCD. Ta có:
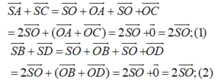
- Từ (1) và (2) suy ra:
Đúng 0
Bình luận (0)
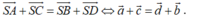
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy, SA = AC. Mặt phẳng qua A vuông góc với SC cắt SB, SC, SD lần lượt tại B', C', D'. Tỉ số giữa thể tích hình chóp S.A'B'C'D' và thể tích hình chóp S.ABCD là:
A. 1/6 B. 1/4
C. 1/3 D. 1/2
Chọn C.
Dễ thấy BD ⊥ SC, nên BD // (AB'C'D'), suy ra BD // B'D'.
Gọi I = AC ∩ BD, J = AC' ∩ SI, khi đó J là trọng tâm của tam giác SAC và J ∈ B'D'.
Suy ra
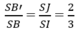
Do đó dễ thấy
Đúng 0
Bình luận (0)
1 tháng 6 2021 lúc 16:42
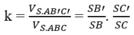
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B có AD=3a, AB=BC=2a. Biết SA⊥(ABCD).
a) Tính khoảng cách từ C đến mặt phẳng (SAD).
b) Tính khoảng cách từ D đến mặt phẳng(SAC).
a, Ta có: \(\left\{{}\begin{matrix}AB\perp SA\left(do:SA\perp\left(ABCD\right)\right)\\AB\perp AD\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow AB\perp\left(SAD\right)\)
Từ C kẻ CH // AB ⇒ CH ⊥ (SAD)
⇒ d (C, (SAD)) = CH = 2a
b, Ta có: \(\left(SAC\right)\cap\left(ABCD\right)=AC\)
Hạ DE ⊥ AC ⇒ DE ⊥ (SAC)
⇒ d(D, (SAC)) = DE
Ta có: AC = 2a√2, AH = HC 2a và HD = a
Xét tam giác HDC vuông tại H, có: \(DC=\sqrt{HD^2+HC^2}=a\sqrt{5}\)
Xét tam giác AHC vuông cân tại H, có: \(\widehat{HAC}=45^o=\widehat{DAE}\)
Xét tam giác ADE vuông tại E, có: \(DE=AD.sin\widehat{DAE}=\dfrac{3a\sqrt{2}}{2}\)
Đúng 2
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết
S
A
⊥
A
B
C
D
A
B
B
C
a
;
A
D
2
a
;
S
A
a
2
. Gọi E là trung điểm của AD. Tính bán kính mặt cầ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết S A ⊥ A B C D A B = B C = a ; A D = 2 a ; S A = a 2 . Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm A, B, C, D, E.
A. a 3 2
B. a
C. a 6 3
D. a 30 6
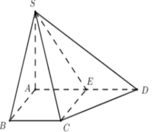
Xét tứ giác ABCE có
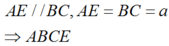
là hình bình hành.
Lại có
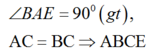
là hình vuông cạnh a.
Bán kính đường tròn ngoại tiếp hình vuông ABCE là
R d = a 2 2
Sử dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp chóp
S.ABCE là:
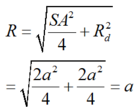
Chọn B.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B; Biết SA vuông góc với mặt đáy, SA
a
2
Tính theo a khoảng cách d từ B đến mặt phẳng (SCD)
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B; 
Biết SA vuông góc với mặt đáy, SA=
a
2
Tính theo a khoảng cách d từ B đến mặt phẳng (SCD)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại C và D,
A
B
C
^
30
o
. Biết ACa,
C
D
a
2
và
S
A
a
3
2
cạnh SA vuông góc với mặt phẳng đáy. Khoảng cách từ...
Đọc tiếp
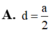
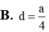
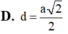
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại C và D, A B C ^ = 30 o . Biết AC=a, C D = a 2 và S A = a 3 2 cạnh SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng (SCD) bằng
A. a 6
B. a 6 2
C. a 6 4
D. a 3 2
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại C và D,
A
B
C
^
30
0
. Biết
A
C
a
,
C
D
a
2
,
S
A
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại C và D, A B C ^ = 30 0 . Biết A C = a , C D = a 2 , S A = a 3 2 và cạnh SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng (SCD) bằng:
