Có bao nhiêu số thực α thuộc ( π , 3 π ) thỏa mãn ∫ π α c o s 2 x d x = 1 4
A. 6
B. 5
C. 4
D. 3
Những câu hỏi liên quan
Có bao nhiêu số thực α thuộc π ; 3 π thỏa mãn ∫ π α cos 2 x d x = 1 4
A. 6
B. 5
C. 4
D. 3
Có bao nhiêu số thực a thuộc
(
π
;
3
π
)
thỏa mãn
∫
π
a
cos
2
x
d
x
1
4
.
Đọc tiếp
Có bao nhiêu số thực a thuộc ( π ; 3 π ) thỏa mãn ∫ π a cos 2 x d x = 1 4 .
Có bao nhiêu số thực a thuộc π ; 3 π thỏa mãn ∫ π a cos 2 x d x = 1 4
A. 6.
B. 5.
C. 4.
D. 3.
trang 40 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 12:46
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)
Đúng 0
Bình luận (0)
Cho góc
α
thỏa mãn:
π
2
α
π
và
sin
α
+
π
.Tính
tan
7
π
3
-
α
A.
3...
Đọc tiếp
Cho góc α thỏa mãn: π 2 < α < π và sin α + π .Tính tan 7 π 3 - α
A. 3 2
B. - 2
C. - 2 2
D. 4 2
Cho góc
α
thỏa mãn
π
2
α
π
và
sin
α
+
π
-
1
3
Tính
tan
7
π
2
-
α
. A.
3
2...
Đọc tiếp
Cho góc α thỏa mãn π 2 < α < π và sin α + π = - 1 3 Tính tan 7 π 2 - α .
A. 3 2
B. - 2
C. - 2 2
D. 4 2
Cho góc
α
thỏa mãn
π
2
α
π
và
sin
α
+
π
-
1
3
. Tính
tan
7
π
2...
Đọc tiếp
Cho góc α thỏa mãn π 2 < α < π và sin α + π = - 1 3 . Tính tan 7 π 2 - α
A. 3 2
B. - 2
C. - 2 2
D. 4 2
Cho góc α thỏa mãn
cos
α
-
5
3
và
π
α
3
π
2
.Tính tanα.
Đọc tiếp
Cho góc α thỏa mãn cos α = - 5 3 và π < α < 3 π 2 .Tính tanα.
Cho góc α thỏa mãn
cos
α
-
12
13
và
π
2
α
π
.Tính tanα.
Đọc tiếp
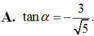
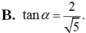
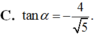
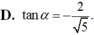
Cho góc α thỏa mãn cos α = - 12 13 và π 2 < α < π .Tính tanα.
