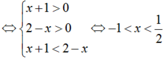Tìm tập nghiệm của phương trình log2(x - 2) + log2(x+1) = 2
![]()
![]()
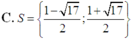
![]()
Tìm tập hợp nghiệm của phương trình log 2 + log 2 ( x - 1 ) = 1
A. {1} B. {2}
C. {1;2} D. {-1;2}
Tìm tập nghiệm S của phương trình l o g 2 ( x - 1 ) + l o g 2 ( x + 1 ) = 3
A . S = - 3 ; 3
B . S = 10
C . S = 3
D . S = - 10 ; 10
Tập nghiệm của bất phương trình log 2 ( x + 1 ) - 2 log 4 ( 5 - x ) < 1 - log 2 ( x - 2 ) là
A. (3;5)
B. (2;3)
C. (2;5)
D. (-4;3)
Tìm tập nghiệm S của phương trình log 2 ( x - 1 ) = log 2 ( 2 x + 1 ) .
A. S = 2
B. S = ∅
C. S = {-2}
D. S = {0}
Tìm tập nghiệm S của bất phương trình l o g 1 2 ( x + 2 ) - l o g 1 2 x > l o g 2 ( x 2 - x ) - 1
A. S = 2 ; + ∞
B. S = 1 ; 2
C. S = 0 ; 2
D. S = ( 1 ; 2 ]
Tìm số nghiệm của phương trình log2 x + log2 (x -1) = 2
A. 0
B. 1
C. 3
D. 2
Gọi S1 là tập nghiệm của bất phương trình log 2 ( x + 5 ) + log 1 2 ( 3 - x ) ≥ 0 và S2 là tập nghiệm của bất phương trình log2(x + 1) ≥ 1. Khẳng định nào dưới đây đúng ?
A. S 1 ∩ S 2 = [ 1 ; 3 )
B. S 1 ∩ S 2 = [ - 1 ; 3 )
C. S 1 ∩ S 2 = - 1 ; 1
D. S 1 ∩ S 2 = 1 ; 3
Tìm các giá trị của tham msố để phương trình log 2 ( m x ) log 2 ( x + 1 ) = 2 có nghiệm duy nhất
A. m < 0
B. m > 4
C. m < 0 ∪ m = 4
D. m < 0 ∪ m ≥ 4
Cho hàm số f(x) = log2x và g(x) = log2(4-x) . Tìm tập nghiệm của bất phương trình f(x + 1) < g(x + 2)
A. S = - ∞ ; 1 2
B. S = - 1 ; 1 2
C. S = (0; 2).
D. S = - ∞ ; 2
Chọn B.
Ta có: f(x + 1) = log2(x + 1) và g(x + 2) = log2(2 - x)
![]()