Có bao nhiêu giá trị nguyên của tham số m để đồ thị của hàm số y = x 3 + ( m + 2 ) x 2 + ( m 2 m - 3 ) x - m 2 cắt trục hoành tại ba điểm phân biệt?
A. 3
B.. 4
C. 1
D. 2
Có bao nhiêu giá trị nguyên của tham số m để đồ thị của hàm số y = x 3 + ( m + 2 ) x 2 + ( m 2 - m - 3 ) x - m 2 cắt trục hoành tại ba điểm phân biệt
A. 3
B. 2
C. 4
D. 1
Chọn đáp án A
Phương pháp
Nhẩm nghiệm của phương trình hoành độ giao điểm, từ đó tìm điều kiện để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.

Để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt thì phương trình x 2 + ( m + 3 ) x + m 2 = 0 phải có hai nghiệm phân biệt khác 1
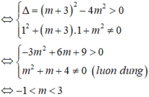
Do đó với -1<m<3 thì đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt
![]()
Cho đồ thị hàm số y=f(x) có đồ thị như hình bên. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = f ( x + 100 ) + m 2 có 5 điểm cực trị?

A. 0.
B. 1.
C. 2.
D. 4.
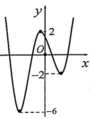
Cho đồ thị hàm số y=f(x) có đồ thị như hình bên. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = f x + 100 + m 2 có 5 điểm cực trị?
A. 0
B. 1
C. 2
D. 4
Chọn đáp án C
Hàm số y=f(x+100) có đồ thị là đồ thị hàm số y=f(x) tịnh tiến sang trái 100 đơn vị
Dựa vào đồ thị ta thấy đồ thị hàm số y=f(x) có 3 điểm cực trị.
Khi tịnh tiến sang trái 100 đơn vị thì số điểm cực trị hàm số y=f(x+100) vẫn là 3 điểm cực trị.

Cho hàm số y = f(x) có đồ thị f'(x) như hình vẽ. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g x = f x 2 + x - 1 + 480 m x 2 + x + 2 nghịch biến trên (0;1)?
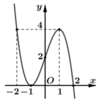
A. 4
B. 6
C. 7
D. 8
Hàm số g(x) nghịch biến trên khoảng (0;1) khi ![]()
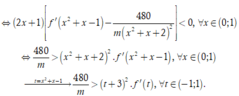
Dựa vào đồ thị, ta có
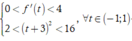
![]()
Theo YCBT 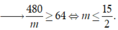
Chọn C.
Cho hàm số y = f(x) có đồ thị f’(x) như hình vẽ. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số g x = f x 2 + x - 1 + 480 m x 2 + x + 2 nghịch biến trên (0; 1)?
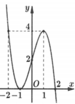
A. 4
B. 6
C. 7
D. 8
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = x 3 − 8 x 2 + ( m 2 + 11 ) x - 2m 2 + 2 có hai điểm cực trị nằm về hai phía của trục Ox.
A. 4
B. 5
C. 6
D. 7
Cho đồ thị hàm số y=f(x) như hình vẽ dưới đây: có bao nhiêu giá trị nguyên của tham số m để hàm số y = f ( x + 2018 ) + m 2 có 5 điểm cực trị
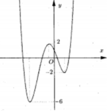
B. 1
C. 2
D. 3
Cho hàm số y = x - 3 x 3 - 3 m x 2 + 2 m 2 + 1 x - m . Có bao nhiêu giá trị nguyên thuộc đoạn [-6;6] của tham số m để đồ thị hàm số có bốn đường tiệm cận?
A.12
B. 9
C. 8
D. 11
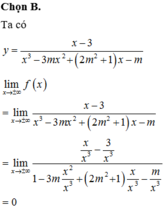
Nên y = 0 là tiệm ngang của đồ thị hàm số.
Vậy để đồ thị hàm số có 4 đường tiệm cận thì đồ thị hàm số phải có 3 đường tiệm cận đứng.
Hay phương trình
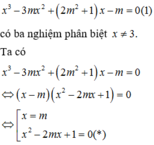
Để phương trình (1) có ba nghiệm phân biệt khác 3 thì m khác 3 và phương trình (*) có hai nghiệm phân biệt khác m và khác 3.
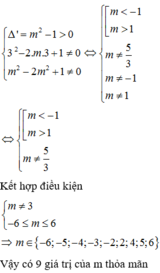
Do đó
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số y = x 3 - ( m + 1 ) x 2 + ( m 2 - 2 ) x - m 2 + 3 có hai điểm cực trị và hai điểm cực trị đó nằm về cùng một phía đối với trục hoành?
A. 4
B. 1
C. 3
D. 2
Chọn đáp án C.
Ta có y ' = 3 x 2 - 2 ( m + 1 ) x + m 2 - 2
trước tiên ta phải có phương trình y ' = 0 có hai nghiệm phân biệt
![]()
![]()
Điều kiện hai điểm cực trị của đồ thị hàm số nằm cùng về một phía đối với trục hoành là y x 1 . y x 2 > 0
⇔ y = 0 có đúng một nghiệm thực.
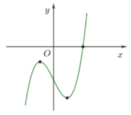
Thử trực tiếp các giá trị của m∈{−1,0,1,2} nhận các giá trị m∈{−1,0,2} để y = 0 có đúng một nghiệm thực.