Cho hàm số f(x) liên tục trên ℝ v à f 2 = 16 , ∫ 0 2 f x d x = 4 . Tính I = ∫ 0 1 x . f ' 2 x d x .
A. 13
B. 12
C. 20
D. 7
Cho hàm số y=f(x) có đạo hàm liên tục trên ℝ thỏa mãn f'(x) -xf(x) = 0, f x > 0 , ∀ x ∈ ℝ và f(0) = 1. Giá trị của f(1) bằng?
A. 1 e .
B. 1 e .
C. e .
D. e.
Cho hàm số y = f(x) có đạo hàm liên tục trên ℝ thỏa mãn f ' x - x f x = 0 , f x > 0 , ∀ x ∈ ℝ và f(0) = 1. Giá trị của f(1) bằng?
A. 1 e
B. 1 e
C. e
D. e
Cho hàm số f(x) liên tục trên ℝ có f(0)=0 và đồ thị hàm số y = f ' ( x ) như hình vẽ bên
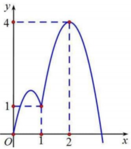
Hàm số y = 3 f ( x ) - x 3 đồng biến trên khoảng
A. 2 ; + ∞
B. - ∞ ; 2
C. (2;0)
D. (1;3)
Đặt g ( x ) = 3 f ( x ) - x 3 . Hàm số ban đầu có dạng y=|g(x)|
Ta có g ' ( x ) = 3 f ' ( x ) - 3 x 2 .
Cho g'(x)=0 ⇔ [ x = 0 x = 1 x = 2

Dễ thấy g(0)=0. Ta có bảng biến thiên
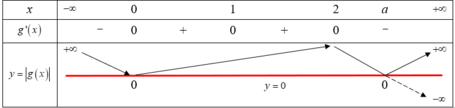
Dựa vào BBT suy ra hàm số y=|g(x)| đồng biến trên khoảng (0;2) và a ; + ∞ với g(a)=0
Chọn đáp án C.
Cho hàm số f(x) liên tục trên ℝ và F(x) là nguyên hàm của f(x), biết ∫ 0 9 f x d x = 9 và F(0) = 3.Tính F(9)
A. F 9 = − 6
B. F 9 = 6
C. F 9 = 12
D. F 9 = − 12
Đáp án C
Ta có:
9 = ∫ 0 9 f x d x = F x = 0 9 F 9 = F 0 ⇒ F 9 = F 0 + 9 = 12.
Cho hàm số y = f(x) liên tục trên ℝ, f(x) >0 ∀ x ∈ ℝ thỏa mãn ln f x + f x - 1 = ln x 2 + 1 e x 2 .Tính I = ∫ 0 1 x f x d x
A. I =-12
B. I =8
C.I =12
D. I =3/4
Cho hàm số f(x) liên tục trên ℝ và F(x) là nguyên hàm của f(x), biết ∫ 0 9 f ( x ) d x = 9 , F(0)=3. Tính F(9).
A. -6.
B. 6.
C. 12.
D. -12.
Cho hàm số f(x) liên tục trên R thỏa mãn điều kiện: f ( 0 ) = 2 3 , f ( x ) > 0 , ∀ x ∈ ℝ và f ( x ) . f ' ( x ) = ( 2 x + 1 ) 1 + f 2 ( x ) , ∀ x ∈ ℝ . Khi đó giá trị f(1) bằng:
![]()
![]()
![]()
![]()
Cho hàm số f(x) liên tục trên ℝ và F(x) là nguyên hàm của f(x), biết ∫ 0 9 f x d x = 9 và F(0) = 3. Giá trị của F(9) bằng
A. F(9) = 6
B. F(9) = 12
C. F(9) = –6
D. F(9) = –12
Cho hàm số f ( x ) liên tục trên ℝ và f ( x ) ≠ 0 với mọi x ∈ ℝ thỏa mãn f ' ( x ) = ( 2 x + 1 ) . f 2 ( x ) v à f ( 1 ) = - 0 , 5 . Biết tổng f ( 1 ) + f ( 2 ) + f ( 3 ) + . . . + f ( 2017 ) = a b ; ( a ∈ ℝ ; b ∈ ℝ ) v ớ i a b tối giản. Mệnh đề nào dưới đây đúng?
A. b - a = 4035
B. a + b = - 1
C. a b < - 1
D. a ∈ - 2017 ; 2017