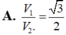
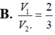
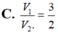
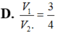
Một khối trụ tròn có 1 đường tròn đáy thuộc mặt bên của 1 hình nón xoay, đáy còn lại thuộc mặt đáy hình nón. Biết chiều cao hình trụ bằng nửa chiều cao hình nón. Tính tỷ số k = V 1 V 2  với V 1 , V 2  tương ứng là thể tích hình trụ và hình nón.

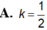
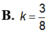
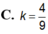
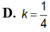
Hình trụ có bán kính đáy r. Gọi O và O' là tâm của hai đường tròn đáy, với O O ' = 2 r .  Một mặt cầu (S ) tiếp xúc với hai đáy hình trụ tại O và O'. Gọi V_C và V_T lần lượt là thể tích khối cầu và khối trụ tương ứng. Khi đó V C V T  bằng:

A. 1/2

B. 3/4

C. 2/3

D. 3/5

Hình trụ có bán kính đáy r. Gọi O và O' là tâm của hai đường tròn đáy, với OO’ = 2r .Một mặt cầu (S ) tiếp xúc với hai đáy hình trụ tại O và O'. Gọi V_C và V_T lần lượt là thể tích khối cầu và khối trụ tương ứng. Khi đó V C V T  bằng:

A.  1 2

B.  3 4

C.  2 3

D.  3 5

Cho hình trụ có hai đáy là các hình tròn (O),  O ' bán kính bằng a, chiều cao hình trụ gấp hai lần bán kính đáy. Các điểm A, B tương ứng nằm trên hai đường tròn (O),  O '  sao cho . Tính thể tích khối tứ diện  A B O O ' theo a

A.  a 3 3

B.  a 3 5 3

C.  2 a 3 3

D.  2 a 3 5 3

Cho hình trụ có hai đáy là các hình tròn (O), (O’) bán kính bằng a, chiều dài hình trụ gấp hai lần bán kính đáy. Các điểm A, B tương ứng nằm trên hai đường tròn (O), (O’) sao cho A B = a 6 . Tính thể tích khối tứ diện ABOO’ theo a?

A.  a 3 3

B.  a 3 5 3

C.  2 a 3 3

D.  2 a 3 5 3

Cho hình trụ có hai đáy là các hình tròn (O), (O’) bán kính bằng a, chiều cao hình trụ gấp hai lần bán kính đáy. Các điểm A, B tương ứng nằm trên hai đường tròn (O), (O’) sao cho A B = a 6 . Tính thể tích khối tứ diện ABOO’ theo a

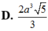
Cho hình chữ nhật ABCD có AB = 3AD. Quay hình chữ nhật ABCD lần lượt quanh AD và AB ta thu được hai hình trụ tròn xoay tương ứng có thể tích V 1 ; V 2 . Hỏi hệ thức nào sau đây là đúng?

A.  V 2 = 3 V 1

B.  V 2 = V 1

C.  V 1 = 3 V 2

D.  V 1 = 9 V 2

Cho hình chữ nhật ABCD có AB=3AD Quay hình chữ nhật ABCD lần lượt quanh AD và AB ta thu được hai hình trụ tròn xoay tương ứng có thể tích V 1 , V 2  Hỏi hệ thức nào sau đây là đúng?AD

A. V 2 = 3 V 1

Lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông cân tại A, BC=2a , cạnh bên AA' = 3a và có hai đáy là hai tam giác nội tiếp hai đường tròn đáy của hình trụ (T). Tính thể tích khối trụ (T).