Các câu hỏi tương tự
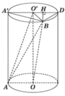
Cho hình trụ có hai đáy là các hình tròn (O),
O
bán kính bằng a, chiều cao hình trụ gấp hai lần bán kính đáy. Các điểm A, B tương ứng nằm trên hai đường tròn (O),
O
sao cho . Tính thể tích khối tứ diện
A
B
O
O
theo a A.
a
3
3
B. ...
Đọc tiếp
Cho hình trụ có hai đáy là các hình tròn (O), O ' bán kính bằng a, chiều cao hình trụ gấp hai lần bán kính đáy. Các điểm A, B tương ứng nằm trên hai đường tròn (O), O ' sao cho . Tính thể tích khối tứ diện A B O O ' theo a
A. a 3 3
B. a 3 5 3
C. 2 a 3 3
D. 2 a 3 5 3
Cho hình trụ có các đáy là hai hình tròn tâm O và O’, bán kính đáy bằng a, chiều cao bằng
a
2
. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O’ lấy điểm O sao cho AB 2a. Tính thể tích của khối tứ diện OO′B′A. A.
a
3
3
2
B.
a
3...
Đọc tiếp
Cho hình trụ có các đáy là hai hình tròn tâm O và O’, bán kính đáy bằng a, chiều cao bằng a 2 . Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O’ lấy điểm O' sao cho AB' = 2a. Tính thể tích của khối tứ diện OO′B′A.
A. a 3 3 2
B. a 3 2 12
C. a 3 2 6
D. a 3 6
Cho hình trụ có các đáy là 2 hình tròn tâm O và O, bán kính đáy bằng chiều cao vào bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O lấy điểm B sao cho AB2a. Thể tích khối tứ diện OOAB theo a là A.
V
3
a
3
8
B.
V
3...
Đọc tiếp
Cho hình trụ có các đáy là 2 hình tròn tâm O và O', bán kính đáy bằng chiều cao vào bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O lấy điểm B sao cho AB=2a. Thể tích khối tứ diện OO'AB theo a là
A. V = 3 a 3 8
B. V = 3 a 3 4 .
C. V = 3 a 3 6 .
D. V = 3 a 3 12 .
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B. Đặt
α
là góc giữa AB và đáy. Biết rằng thể tích khối tứ diện OO’AB đạt giá trị lớn nhất. Khẳng định nào sau đây là đúng ? Tính bán kính mặt cầu ngoại tiếp hình chóp theo a. A.
tan
α
2
B.
tan
α
1...
Đọc tiếp
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B. Đặt α là góc giữa AB và đáy. Biết rằng thể tích khối tứ diện OO’AB đạt giá trị lớn nhất. Khẳng định nào sau đây là đúng ? Tính bán kính mặt cầu ngoại tiếp hình chóp theo a.
A. tan α = 2
B. tan α = 1 2
C. tan α = 1 2
D. tan α = 1
Cho hình trụ có chiều cao h a
3
, bán kính đáy r a. Gọi O,O’ lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai dường thẳng AB và OO’ chéo nhau và góc giữa hai đường thẳng AB với OO’ bằng 300. Khoảng cách giữa hai đường thẳng AB và OO’ bằng : A.
a
6
B.
a
6...
Đọc tiếp
Cho hình trụ có chiều cao h = a 3 , bán kính đáy r = a. Gọi O,O’ lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai dường thẳng AB và OO’ chéo nhau và góc giữa hai đường thẳng AB với OO’ bằng 300. Khoảng cách giữa hai đường thẳng AB và OO’ bằng :
A. a 6
B. a 6 2
C. a 3
D. a 3 2
Cho hình trụ
T
có chiều cao bằng đường kính đáy, hai đáy là các hình tròn
O
;
r
và
O
;
r
. Gọi A là điểm di động trên đường tròn
O
;
r
v à B là điểm di động trên đường tròn
O
;
r...
Đọc tiếp
Cho hình trụ T có chiều cao bằng đường kính đáy, hai đáy là các hình tròn O ; r và O ' ; r . Gọi A là điểm di động trên đường tròn O ; r v à B là điểm di động trên đường tròn O ' ; r sao cho AB không là đường sinh của hình trụ T . Khi thể tích khối tứ diện O O ' A B đạt giá trị lớn nhất thì đoạn thẳng AB có độ dài bằng
A. 3 r
B. 2 + 2 r
C. 6 r
D. 5 r
Một hình trụ có bán kính r và chiều cao h r√3.a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.b) TÍnh thể tích khối trụ tạo nên bởi hình trụ đã cho.c) Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng 300. TÍnh khoảng cách giữa đường thẳng AB và trục của hình trụ
Đọc tiếp
Một hình trụ có bán kính r và chiều cao h = r√3.
a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
b) TÍnh thể tích khối trụ tạo nên bởi hình trụ đã cho.
c) Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng 300. TÍnh khoảng cách giữa đường thẳng AB và trục của hình trụ
Cho hình trụ có đáy là hai đường tròn
O
;
R
v
à
O
;
R
, chiều cao bằng đường kính đáy. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O lấy điểm B. Thể tích của khối tứ diện
O
O
A
B
có giá trị lớn nhất bằng: A. ...
Đọc tiếp
Cho hình trụ có đáy là hai đường tròn O ; R v à O ' ; R , chiều cao bằng đường kính đáy. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O' lấy điểm B. Thể tích của khối tứ diện O O ' A B có giá trị lớn nhất bằng:
A. R 3 2
B. 3 R 3 3
C. R 3 6
D. R 3 3
Cho hình trụ có chiều cao
h
a
3
bán kính
r
a
. Gọi O và O’ lần lượt là tâm của hai hình tròn đáy. Hai điểm A,B thuộc hai đường tròn đáy sao cho
A
B
2
a
. Tính số đo góc giữa hai đường thẳng AB và OO’ A.
A
B
,
O
O...
Đọc tiếp
Cho hình trụ có chiều cao h = a 3 bán kính r = a . Gọi O và O’ lần lượt là tâm của hai hình tròn đáy. Hai điểm A,B thuộc hai đường tròn đáy sao cho A B = 2 a . Tính số đo góc giữa hai đường thẳng AB và OO’
A. A B , O O ' = 30 0
B. A B , O O ' = 60 0
C. A B , O O ' = 45 0
D. A B , O O ' = 90 0