Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Gọi I là trung điểm AB. Mặt phẳng I B ' D ' cắt hình hộp theo thiết diện là hình gì?
A.Hình bình hành
B. Hình thang
C. Hình chữ nhật
D. Tam giác
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = 2 a , A D = a , A A ' = a 3 . Gọi M là trung điểm cạnh AB. Khoảng cách từ D đến mặt phẳng (B'MC) bằng
A. a 21 7
B. 2 a 21 7
C. 3 a 21 7
D. a 21 14
Khoảng cách từ D đến (B'MC)
gấp hai lần khoảng cách từ B đến (B'MC)
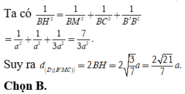
Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật. Tâm của mặt cầu (S) là:
A. Tâm của hình hộp chữ nhật
B. Tâm của một mặt bên của hình hộp chữ nhật
C. Trung điểm của một cạnh của hình hộp chữ nhật
D. Một đỉnh bất kì của hình hộp chữ nhật
Chọn A.
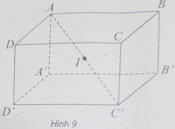
(h.9) Tâm của hình hộp chữ nhật cách đều 8 đỉnh của hình hộp nên tâm của mặt cầu (S) chính là tâm của hình hộp chữ nhật.
Cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, hình chiếu của A' lên đáy (ABCD) trùng với trung điểm của cạnh AD. Biết rằng AB = a, AD = 2a và thể tích hình hộp đã cho bằng 2 a 3 . Khoảng cách từ B đến mặt phẳng (A'DCB') bằng:
A. 2 a 6 B. 2 a 3
C. 3 a 3 D. a 2
Chọn D.
Gọi H là trung điểm của cạnh AD. Kẻ HI vuông góc với A'D tại I. Khi đó d(B,(A'DCB')) = d(A,(A'DCB')) = 2d(H,(A'DCB')) = 2HI.
Cho hình hộp chữ nhật ABCD.A'B'C'D' . Gọi I là trung điểm AB. Mặt phẳng (IB'D') cắt hình hộp theo thiết diện là hình gì?
A.Hình bình hành.
B. Hình thang.
C. Hình chữ nhật.
D. Tam giác.
Chọn B.
Ta có (IB'D') và ABCD có I là một điểm chung.
B ' D ' ⊂ ( I B D ) B D ⊂ ( A B C D ) B ' D ' / / B D ⇒ ( I B D ) ∩ ( A B C D ) = I J / / ( J ∈ A D )
Thiết diện là hình thang IJB'D'
1.Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi A',B' lần lượt là trung điểm của SA,SB . Đường thẳng A' B' song song với mặt phẳng nào dưới đây?
A. (SAB).
B. ( ABCD) .
C. (SAD).
D. (SBC).
2.Cho hình hộp ABCD.A' B' C' D' . Mặt phẳng ( ABA') song song với:
A. ( AA'C') .
B. (CC'D').
C. ( ADD').
D. (BB'A').
Cho hình hộp chữ nhật ABCD.A'B'C'D' có A B = B C = a ; A ' A = a 3 . Gọi I là giao điểm của AD' và A’D ; H là hình chiếu của I trên mặt phẳng A ' B ' C ' D ' , K là hình chiếu của B lên mặt phẳng C A ' B ' . Tính thể tích khối tứ diện IHBK ?
A. a 3 3 4
B. a 3 3 6
C. a 3 3 16
D. a 3 3 8
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = B C = a , A ' A = a 3 . Gọi I là giao điểm của A D ' và A ' D ; H là hình chiếu của I trên mặt phẳng A ' B ' C ' D ' , K là hình chiếu của B lên mặt phẳng C A ' B ' . Tính thể tích khối tứ diện IHBK ?
A. a 3 3 4
B. a 3 3 6
C. a 3 3 16
D. a 3 3 8
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi M và N theo thứ tự là trung điểm của A’B’ và B’C’. Tính tỉ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’
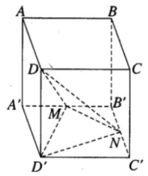
Thể tích khối chóp D’.DMN bằng thể tích khối chóp D.D’MN
Ta có: S D ' MN = S A ' B ' C ' D ' - S D ' A ' M + S D ' C ' N + S B ' MN
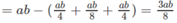
Thể tích khối chóp
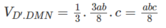
Từ đó suy ra tỷ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng 1/8
cho hình chóp SABCD đáy ABCD là hình chữ nhật AB= a ,AD=2a,SA=SB=SC=SD=2a gọi O là giao điểm của AC và BD
a chứng minh mặt phẳng SAC vuông góc với mặt phẳng ABCD
b tính khoảng cách từ O->mặt phẳng SCD
c gọi M,N lần lượt là trung điểm của các cạnh SA và BC tính sin góc MN,CSBD