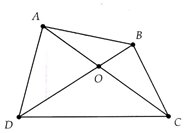
Có hình vẽ : 

Dễ thấy S_ABCD = \(\frac{1}{2}\left(AH+CK\right).BD\)

mà lại có \(AH=AO.sin\alpha\) ; \(CK=OC.sin\alpha\)

=> S_ABCD = \(\frac{1}{2}\sin\alpha.AC.BD\)

Khi 2 đường chéo vuông góc với nhau thì 

\(H\equiv O\equiv K\Rightarrow AH=AO=CK\)

hay \(sin\alpha=1\)

Khi đó \(S_{ABCD}=\frac{1}{2}mn\)(đpcm) 

a, Giả sử tam giác ABC có  A ^ < 90 0  kẻ đường cáo BH. Ta có BH=AB.sin A ^

=>  S ∆ A B C = 1 2 A C . B H =  1 2 A B . A C . sin A

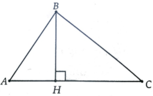
b, Giả sử tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O có  A O B ^ = α < 90 0 . Kẻ AH ⊥ BD, tại H và CK ⊥ BD tại K

Ta có: AH = OA.sinα

=>  S A B D = 1 2 B D . A H =  1 2 B D . O A . sin α

Tương tự:  S C B D = 1 2 B D . C K =  1 2 B D . O C . sin α

=>  S A B C D = S A B D + S C B D =  1 2 B D . O A . sin α +  1 2 B D . O C . sin α =  1 2 B D . A C . sin α

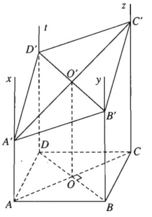
a) Ta có hai mặt phẳng song song là: (Ax, AD) // (By, BC)

Hai mặt phẳng này bị cắt bởi mặt phẳng (β) nên ta suy ra các giao tuyến của chúng phải song song nghĩa là A′D′ // B′C′.

Tương tự ta chứng minh được A′B′ // D′C′. Vậy A', B', C', D' là hình bình hành. Các hình thang AA'C'C và BB'D'D đều có OO' là đường trung bình trong đó O là tâm của hình vuông ABCD và O' là tâm của hình bình hành A',B',C',D'. Do đó: AA′ + CC′ = BB′ + DD′ = 2OO′

b) Muốn hình bình hành A',B',C',D' là hình thoi ta cần phải có A'C' ⊥ B'D'. Ta đã có AC ⊥ BD. Người ta chứng minh được rằng hình chiếu vuông góc của một góc vuông là một góc vuông khi và chỉ khi góc vuông đem chiếu có ít nhất một cạnh song song với mặt phẳng chiếu hay nằm trong mặt chiếu. Vậy A', B', C', D' là hình thoi khi và chỉ khi A'C' hoặc B'D' song song với mặt phẳng (α) cho trước. Khi đó ta có AA' = CC' hoặc BB' = DD'.

c) Muốn hình bình hành A', B', C', D' là hình chữ nhật ta cần có A'B' ⊥ B'C', nghĩa là A'B' hoặc B'C' phải song song với mặt phẳng (α)(α). Khi đó ta có AA' = BB' hoặc BB' = CC', nghĩa là hình bình hành A', B', C', D' có hai đỉnh kề nhau cách đều mặt phẳng (α) cho trước.

Bài 1: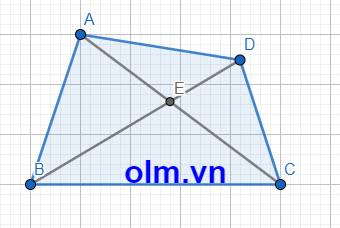 

Gọi E là giao điểm của hai đường chéo AC và BD 

Xét tam giác AEB ta có: AE + BE > AB (trong một tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)

Xét tam giác DEC ta có: DE + CE > DC (trong một tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)

Cộng vế với vế ta có: AE + BE + DE + CE > AB + DC 

                                  (AE + CE) + (BE + DE) > AB + DC

                                     AC + BD > AB + DC 

Tương tự ta có AC + BD > AD + BC 

Kết luận: Trong một tứ giác tổng hai đường chéo luôn lớn hơn tổng hai cạnh đối.

Nửa chu vi của tứ giác ABCD là: \(\dfrac{AB+BC+CD+DA}{2}\)

Theo chứng minh trên ta có:

 \(\dfrac{AB+BC+CD+DA}{2}\)< \(\dfrac{\left(AB+CD\right)\times2}{2}\) = AB + CD (1)

Vì trong một tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại nên ta có:

AB + AD > BD 

AB + BC > AC

BC + CD > BD 

CD + AD > AC 

Cộng vế với vế ta có:

(AB + BC + CD + DA)\(\times\)2 > (BD + AC ) \(\times\) 2

⇒AB + BC + CD + DA > BD + AC  (2)

Kết hợp (1) và (2) ta có:

Tổng hai đường chéo của tứ giác lớn hơn nửa chu vi của tứ giác nhưng nhỏ hơn chu vi của tứ giác

Bài : 2 Góc C = 180⁰ - 60⁰ = 120⁰

          Tổng bốn góc của tứ giác là 360⁰

           Ta có: Góc B của tứ giác ABCD là:

              360⁰ - (70⁰ + 80⁰ + 120⁰) = 90⁰

Câu b chứng minh như bài 1

Bài 1:

a) Sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác OAB, OBC,OCD và ODA.

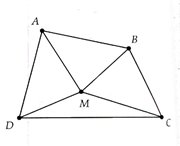
b) Chứng minh tổng hai đường chéo lớn hơn nửa chu vi tứ giác sử dụng kết quả của a).

Chứng minh tổng hai đường chéo nhỏ hơn chu vi tứ giác sử dụng tính chất tổng hai cạnh trong một tam giác thì lớn hơn cạnh còn lại cho các tam giác ABC, ADC, ABD và CBD

Bài 3:

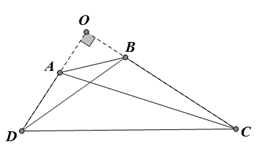
Gọi O là giao điểm AD và BC.

Ta có $\hat{C}+\stackrel{⌢}{D}={90}^0$ nên $\hat{O}={90}^0$

Áp dụng định lí Py – ta – go,

Ta có 

$A{C}^2=O{A}^2+O{C}^2.$

$B{D}^2=O{B}^2+O{D}^2$

Nên $A{C}^2+B{D}^2=\left(O{A}^2+O{B}^2\right)+\left(O{C}^2+O{D}^2\right)=A{B}^2+C{D}^2$