Gọi ∆ là tiếp tuyến của đường cong C : y = x 2 - x + 1 x + 1 . Biết rằng ∆ qua điểm (-1;0). Tính khoảng cách d từ điểm M(1;-1) đến ∆
A. d = 2 5
B. d = 1 5
C. d = 1
D. d = 2
Cho đường cong (C) có phương trình y = x − 1 x + 1 . Gọi M là giao điểm của (C) với trục tung. Tiếp tuyến của (C) tại M có phương trình là
A. y = − 2 x − 1
B. y = 2 x + 1
C. y = 2 x − 1
D. y = x − 2
Cho đường cong (C) có phương trình y = x - 1 x + 1 . Gọi M là giao điểm của (C) với trục tung. Tiếp tuyến của (C) tại M có phương trình là:
![]()
![]()
![]()
![]()
Cho đường cong (C) có phương trình y = x - 1 x + 1 . Gọi M là giao điểm của (C) với trục tung. Tiếp tuyến của (C) tại M có phương trình là:
A. y = - 2 x - 1
B. y = 2 x + 1
C. y = 2 x - 1
D. y = x - 2
cho đường cong (C) là đồ thị của Hàm Số y = 2x^3 - 2x^2 - 4x + 1. viết phương trình tiếp tuyến của đường cong C tại điểm có hoành độ x=0
\(y'=6x^2-4x-4\)
\(y'\left(0\right)=-4\)
\(y\left(0\right)=1\)
Do đó pt tiếp tuyến tại điểm có hoành độ x=0 là:
\(y=-4\left(x-0\right)+1\Leftrightarrow y=-4x+1\)
Cho đường cong (C) là đồ thị của hàm số y = x^2 - 4x + 3. Viết pt tiếp tuyến của đường cong đó. a) tại điểm Mo = (-2, 15) b) tại điểm có tung độ x = 3 c) k = 4
\(y'=2x-4\)
a.
\(y'\left(-2\right)=2.\left(-2\right)-4=-8\)
Phương trình tiếp tuyến:
\(y=-8\left(x+2\right)+15\Leftrightarrow y=-8x-1\)
b.
Gọi \(x_0\) là hoành độ tiếp điểm
\(\Rightarrow x_0^2-4x_0+3=3\Rightarrow x_0^2-4x_0=0\)
\(\Rightarrow\left[{}\begin{matrix}x_0=0\Rightarrow y'\left(0\right)=-4\\x_0=4\Rightarrow y'\left(4\right)=4\end{matrix}\right.\)
Có 2 tiếp tuyến: \(\left[{}\begin{matrix}y=-4\left(x-0\right)+3\\y=4\left(x-4\right)+3\end{matrix}\right.\) \(\Leftrightarrow...\)
c.
Gọi \(x_0\) là hoành độ tiếp điểm \(\Rightarrow y'\left(x_0\right)=k=4\)
\(\Rightarrow2x_0-4=4\Rightarrow x_0=4\)
\(\Rightarrow y\left(4\right)=3\)
Pttt: \(y=4\left(x-4\right)+3\Leftrightarrow y=4x-13\)
Lập phương trình tiếp tuyến của đường cong (C): y = x3 + 3x2 – 8x + 1, biết tiếp tuyến đó song song với đường thẳng Δ: y = x + 2017?
A. y = x + 2018.
B. y = x + 4.
C. y = x – 4; y = x + 28.
D. y = x - 2018.
Chọn C.
Đạo hàm: y’ = 3x2 + 6x – 8.
Tiếp tuyến cần tìm song song với đường thẳng Δ: y = x + 2017 nên hệ số góc của tiếp tuyến là 1.
Ta có phương trình 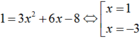
Tại M(1; -3). Phương trình tiếp tuyến là y = x – 4.
Tại N(-3; 25). Phương trình tiếp tuyến là y = x + 28.
Cho đường cong (C) : y = 3x + 1 / 1 - x 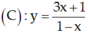
Số tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng (Δ): 2x + 2y – 9 = 0.
A. 1
B. 2
C. 3
D. 4
Chọn A.
Tập xác định D = R \ {1}. Ta có 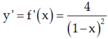
![]()
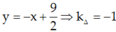
Vì tiếp tuyến vuông góc với Δ nên, ![]()
Gọi N(xo; yo) là tọa độ tiếp điểm của tiếp tuyến, ta có f’(xo) = ktt 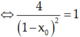
⇔ (xo – 1)2 = 4 ⇔ xo = 3 ∨ xo = -1.
Với xo = 3 ⇒ y = -5, phương trình tiếp tuyến tại điểm này là:
⇔ y = -1(x – 3) – 5 ⇔ y = -x – 2
Với xo = -1 ⇒ y = -1, phương trình tiếp tuyến tại điểm này là:
⇔ y = -1(x + 1) – 1 ⇔ y = -x – 2.
Cho hàm số y=f(x)=x3-3x2+1
a)Xác định điểm I thuộc đồ thị (C) của hàm số đã cho biết rằng hoành độ của điểm I là nghiệm của Phương trình f’’(x)= 0.
b)Viết công thức chuyển hệ tọa độ trong phép tịnh tiến vectơ OI và viết Phương trình của đường cong với hệ tọa độ IXY. Từ đó suy ra bằng I là tâm đối xứng đường cong (C).
c)Viết phương trình tiếp tuyến của đường cong (C) tại điểm I đối với hện tọa độ Oxy. Chứng minh rằng trên khoảng (-∞;1) đường cong (C) nằm phía dưới tiếp tuyến tại I của (C) và trên khoảng (1; +∞) đường cong (C) nằm phía trên tiếp tuyến đó.
Đường thẳng y = 3x + m là tiếp tuyến của đường cong y = x 3 + 2 khi m bằng
A. 1 hoặc -1
B. 3 hoặc -3
C. 4 hoặc 0
D. 2 hoặc -2
Chọn C
y ' = 3 x 2 . Đường thẳng y = 3x + m là tiếp tuyến của đường cong y = x 3 + 2
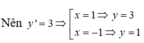
Tiếp tuyến của đường cong tại A(1;3) là y = 3(x - 1) + 3 hay y = 3x.
Tiếp tuyến của đường cong tại B(-1;1) là y = 3(x + 1) + 1 hay y = 3x + 4.
Do đó m ∈ {0; 4}