Chứng minh rằng ba điểm C, B, D ở hình dưới thẳng hàng.

Những câu hỏi liên quan
Cho hình dưới (hình 65a). Chứng minh rằng ba điểm B, K, C thẳng hàng
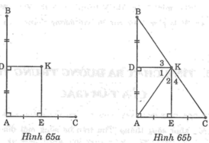
Nối KA, KB, KC (hình 65b).
Vì KD là đường trung trực của AB nên:
KA = KB (tính chất đường trung trực)
Suy ra: ΔKAB cân tại K
Do đó KD là đường phân giác của ∠(AKB)
Suy ra: ∠K1 = ∠K3 ⇒ ∠(AKB) = 2 ∠K1 (1)
Vì KE là đường trung trực của AC nên:
KA = KC (tính chất đường trung trực)
Do đó, tam giác AKC cân tại K. Suy ra KE là đường phân giác của ∠(AKC)
Suy ra: ∠K2 = ∠K4 ⇒ ∠(AKC) = 2 ∠K2 (2)
Ta có: KD ⊥ AB (gt) và AC ⊥ AB (gt)
Suy ra: KD // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song nhau)
Lại có: KE ⊥ AC (gt)
Suy ra: KE ⊥ KD (quan hệ giữa tính vuông góc và tính song song)
Hay: ∠(DKE) = 90o⇒ ∠K1 +∠K2 = 90o
Từ (1) và (2) suy ra: ∠(AKB) + ∠(AKC) = 2∠K1 + 2∠K2
= 2.( ∠K1 +∠K2 ) = 2.90o = 180o.
Vậy B, K, C thẳng hàng.
Đúng 0
Bình luận (0)
Cho hình 88.
Chứng minh rằng BC // OO’ và ba điểm C, B, D thẳng hàng.
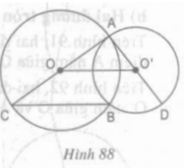
Xét tam giác ABC có:
OA = OB = OC = bán kính đường tròn (O)
Mà BO là trung tuyến của tam giác ABC
⇒ ∆ABC vuông tại B ⇒ AB ⊥ BC (1)
Lại có OO’ là đường trung trực của AB
⇒ AB ⊥ OO' (2)
Từ (1) và (2) ⇒ OO’ // BC
Chứng minh tương tự ta có ∆ABD vuông tại B ⇒ AB ⊥ BD (3)
Từ (1) và (3) ⇒ B, C, D thẳng hàng.
Đúng 0
Bình luận (0)
Cho hình 51: Chứng minh ba điểm B, C, D thẳng hàng.
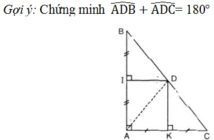
Hình 51
QUẢNG CÁOTừ hình vẽ ta có:
+ DK là đường trung trực của AC ⇒ DA = DC.
+ DI là đường trung trực của AB ⇒ DA = DB.
+ Ta có : DI // AC (vì cùng ⏊ AB)
Mà DK ⏊ AC ⇒ DK ⏊ DI 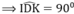
+ Xét ∆ADK và ∆CDK có:
AD = DC
AK = CK (gt)
DK chung
⇒ ∆ADK = ∆CDK (c.c.c)
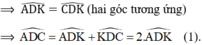
+ Xét ∆ADI và ∆BDI có :
AD = BD
AI = BI (gt)
DI chung
⇒ ∆ADI = ∆BDI (c.c.c)
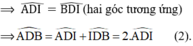
Từ (1) và (2) suy ra
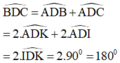
Vậy B, D, C thẳng hàng.
Đúng 0
Bình luận (0)
Cho hình 72. Trong đó ABCD là hình bình hành
a) Chứng minh rằng AHCK là hình bình hành
b) Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A, O, C thẳng hàng.
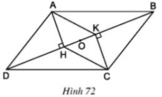
a)+ ABCD là hình bình hành
⇒ AD // BC và AD = BC.
⇒ ∠ADH = ∠CBK (Hai góc so le trong).
Hai tam giác vuông AHD và CKB có:
AD = BC
∠ADH = ∠CBK
⇒ ΔAHD = ΔCKB (cạnh huyền, góc nhọn)
⇒ AH = CK
+ AH ⊥ BD; CK ⊥ BD ⇒ AH // CK
Tứ giác AHCK có AH // CK, AH = CK nên là hình bình hành.
b) Hình bình hành AHCK có O là trung điểm HK
⇒ O = AC ∩ HK ⇒ A, C, O thẳng hàng.
Đúng 1
Bình luận (0)
vẽ 5 điểm A , B, C, D, E trong đó A, B, C thẳng hàng, ba điểm A, B, D không thẳng hàng và ba điểm A, B, E thẳng hàng.
a, nêu cách vẽ hình và giải thích
b ) Chứng minh rằng 4 điểm A, B, C, E cùng thuộc 1 đường thẳng d.
c ) Hai đường thẳng AB và DE có phải là 2 đường thẳng trùng nhau không?
d ) Có bao nhiêu đường thẳng đi qua từng cặp điểm trong số 5 điểm đã cho ?
Cho ba điểm A,B và C thẳng hàng;D là điểm mà C nằm giữa A và D
a)Chứng minh ba điểm B,C,D thẳng hàng
b)Biết rằng B nằm giữa A và C. Hãy chỉ ra C nằm giữa những điểm nào?
Bài 1: Cho hình thang ABCD (AB // CD) có . Hai tia phân giác của góc C và D cắt nhau tại điểm E. Chứng minh rằng ba điểm A, E, B thẳng hàng.
Cho hình 88.
a) Hãy xác định vị trí tương đối của hai đường tròn (O) và (O’).
b) Chứng minh rằng BC // OO’ và ba điểm C, B, D thẳng hàng.
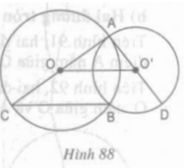
a) Hai đường tròn (O) và (O’) cắt nhau
b) Xét tam giác ABC có:
OA = OB = OC = bán kính đường tròn (O)
Mà BO là trung tuyến của tam giác ABC
⇒ ∆ABC vuông tại B ⇒ AB ⊥ BC (1)
Lại có OO’ là đường trung trực của AB
⇒ AB ⊥ OO' (2)
Từ (1) và (2) ⇒ OO’ // BC
Chứng minh tương tự ta có ∆ABD vuông tại B ⇒ AB ⊥ BD (3)
Từ (1) và (3) ⇒ B, C, D thẳng hàng.
Đúng 0
Bình luận (0)
ho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. Đường trung trực của đoạn thẳng OA cắt Ox ở D, đường trung trực của đoạn thẳng OB cắt Oy ở E. Gọi C là giao điểm của hai đường trung trực đó. Chứng minh rằng:
Ba điểm A, B, C thẳng hàng.
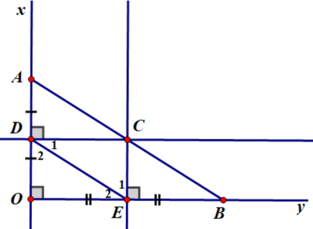
Chứng minh tương tự như d suy ra CB // DE.
Do đó theo tiên đề Ơ-clit ta suy ra hai đường thẳng BC và CA trùng nhau hay A, B, C thẳng hàng.
Đúng 0
Bình luận (0)





