Hỏi a và b thỏa mãn điều kiện nào để hàm số ![]() có đồ thị dạng như hình vẽ?
có đồ thị dạng như hình vẽ?

A. a>0, b<0
B. a<0, b>0
C. a<0, b<0
D. a>0, b>0
Cho đồ thị hàm số y = f(x) có đạo hàm trên R thỏa mãn f(2) = f(-2) = 0 và đồ thị hàm số y = f'(x) có dạng như hình vẽ. Hàm số y = f ( x ) 2 nghịch biến trên khoảng nào trong các khoảng sau?
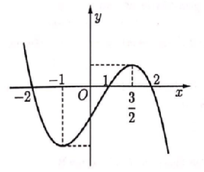
A. - 1 ; 3 2
B. (-2;-1)
C. (-1;1)
D. (1;2)
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [ 0 ; d ] . Khẳng định nào sau đây là khẳng định đúng?

A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)
Cho hàm số y=f(x) có đạo hàm trên R thỏa mãn f(-1)= f(3)= 0 và đồ thị hàm số y=f' (x) có dạng như hình vẽ. Hàm số y= [ f ( x ) ] 2 nghịch biến trên khoảng nào trong các khoảng sau?
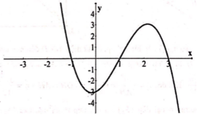
A. (-2;1).
B. (1;2).
C. (0;4).
D. (-2;2).
Cho hàm số y=f(x) có đồ thị như hình vẽ bên:
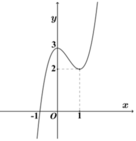
Điều kiện của m để phương trình f x = m có 4 nghiệm phân biệt x 1 , x 2 , x 3 , x 4 thỏa mãn x 1 ≤ - 1 2 x 2 < x 3 ≤ 1 2 x 4 là:
A. m ∈ 2 ; 3
B. m ∈ 2 ; 3
C. m ∈ [ 5 2 ; 3 )
D. m ∈ [ 2 ; 5 2 )
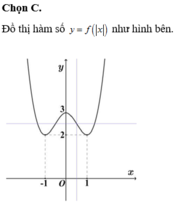
Đồ thị hàm số có điểm uốn là trung điểm của 2 đường cực trị I 1 2 ; 5 2
Số nghiệm của phương trình f(|x|)=m là số giao điểm của đồ thị hàm số y=f(|x|) và đường thẳng y=m. Để phương trình có 4 nghiệm thỏa mãn điều kiện đề bài thì 5 2 ≤ m < 3
Cho a, b là các số thực dương khác 1. Các hàm số y = a x và y = b x có đồ thị như hình vẽ bên. Đường thẳng bất kỳ song song với trục hoành và cắt đồ thị hàm số y = a x , y = b x , trục tung lần lượt tại M, N, A đều thỏa mãn AN = 2AM. Mệnh đề nào sau đây đúng?
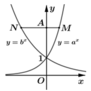
A. b = 2a
B. a 2 = b
C. a b = 1 2
D. a b 2 = 1
Gọi A(0;t) với t > 0. Suy ra 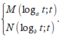
Theo giả thiết AN = 2AM nên suy ra
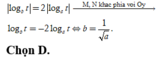
Biết đồ thị hàm số y = x 4 + b x 2 + c chỉ có một điểm cực trị là điểm có tọa độ 0 ; − 1 thì b và c thỏa mãn điều kiện nào?
A. b ≥ 0 và c = − 1
B. b < 0 và c = − 1
C. b ≥ 0 và c > 0
D. b ≥ 0 và c tùy ý
Đáp án là A
y ' = 4 x 3 + 2 b x , c h o y ' = 0 ⇔ x = 0 x 2 = − b 2 *
Đồ thị chỉ có một điểm cực trị nên phương trình (*) có một nghiệm hoặc vô nghiệm, suy ra: b ≥ 0.
mà điểm 0 ; − 1 là điểm cực trị của đồ thị nên c = − 1
Biết đồ thị hàm số y = x 4 + b x 2 + c chỉ có một điểm cực trị là điểm có tọa độ 0 ; − 1 thì b và c thỏa mãn điều kiện nào ?
A. b ≥ 0 v à c = − 1
B. b < 0 v à c = − 1
C. b ≥ 0 v à c > 0
D. b > v à c tùy ý
Đáp án A
Do hàm số chỉ có một điểm cực trị có tọa độ 0 ; − 1 nên c = − 1 ⇒ Loại C,D
Lại có y ' = 4 x 3 + 2 b x = 2 x 2 x 2 + b 1 nghiệm duy nhất x=0 khi và chỉ khi 2 x 2 + b ≥ 0 ⇔ b ≥ 0.
Cho hàm số y = f(x) có đạo hàm trên ℝ , thỏa mãn f − 1 = f 3 = 0 và đồ thị của hàm số y = f ' x có dạng như hình dưới đây.
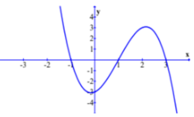
Hàm số y = f x 2 nghịch biến trên khoảng nào trong các khoảng sau?
A. (1;2)
B. (-2;1)
C. (0;4)
D. (-2;2)
Cho hàm số y = m x 2 − 2(m − 1)x + 1 (m ≠ 0) có đồ thị (Cm). Tịnh tiến ( C m ) qua trái 1 đơn vị ta được đồ thị hàm số ( C m ' ). Giá trị của m để giao điểm của ( C m ) và ( C m ' ) có hoành độ x = 14 thỏa mãn điều kiện nào dưới đây?
A. 1 < m < 5
B. m > 4
C. 0 < m < 2
D. −2 < m < 0