Đáp án A
Phương pháp: Quan sát đồ thị hàm số và đánh giá dấu của các hệ số a, b.
Cách giải: Đồ thị hàm số ![]() có
có ![]()
![]()

(C) có ba cực trịó y’ = 0 có 3 nghiệm phân biệt ![]() vì a>0
vì a>0
Vậy a>0, b<0
Đáp án A
Phương pháp: Quan sát đồ thị hàm số và đánh giá dấu của các hệ số a, b.
Cách giải: Đồ thị hàm số ![]() có
có ![]()
![]()

(C) có ba cực trịó y’ = 0 có 3 nghiệm phân biệt ![]() vì a>0
vì a>0
Vậy a>0, b<0
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [ 0 ; d ] . Khẳng định nào sau đây là khẳng định đúng?

A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)
Cho a > 0 , b > 0 , b ≠ 0 . Đồ thị các hàm số y = a x và y = log b x cho như hình vẽ bên. Mệnh đề nào sau đây là đúng
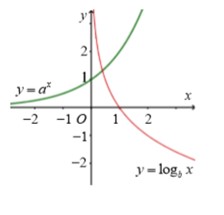
A. a>1, 0<b<1
B. 1>a>0; b>1
C. 0<a<1; 0<b<1
D. a>1; b>1
Cho a > 0, b > 0, a ≠ 1, b ≠ 1 . Đồ thị hàm số y = a x và y = log b x được xác định như hình vẽ bên. Mệnh đề nào sau đây là đúng?
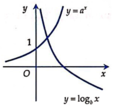
A. a > 1 ; 0 < b < 1.
B. 0 < a < 1 ; b > 1.
C. 0 < a < 1 ; 0 < b < 1.
D. a > 1 ; b > 1.
Đồ thị hàm số y = ax3 + bx2 + cx + d (a, b, c, d là các hằng số thực và a ≠ 0) như hình vẽ.
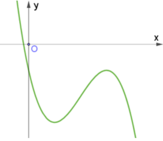
Khẳng định nào đúng
A. b > 0, c > 0
B. b < 0, c < 0
C. b < 0, c > 0
D. b > 0, c < 0
Hình vẽ bên giống với đồ thị của hàm số nào nhất trong bốn đáp án A,B,C,D dưới đây, biết hàm số đó có dạng y = ax 4 + bx 2 + c , a ≠ 0 .
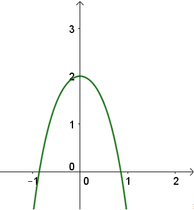
A. y = − x 4 + 2 x 2 + 2
B. y = − x 4 + 2 x 2 − 2
C. y = − x 4 − 2 x 2 + 2
D. y = x 4 − 2 x 2 + 2
Hàm số y = b x - c x - a a ≠ 0 ; a , b , c ∈ ℝ có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
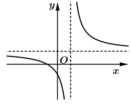
A. a > 0, b > 0, c - ab < 0
B. a > 0, b > 0, c - ab > 0
C. a > 0, b > 0, c - ab = 0
D. a > 0, b < 0, c - ab < 0
Cho 0 < a ≠ 1 và 0 < b ≠ 1 . Đồ thị hàm số y = a x và y = log b x được xác định như hình vẽ dưới đây. Mệnh đề nào sau đây đúng?

A. a >1, b >1
B. a >1, 0 <b <1
C. 0 <a <1, b >1
D. 0 <a <1, 0 <b <1
Cho hàm số y = f ( x ; m ) có đồ thị hàm số y = f ' ( x ; m ) như hình vẽ
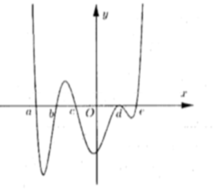
Biết f ( a ) > f ( c ) > 0 ; f ( b ) < 0 < f ( e ) Hỏi hàm số y = f ( x , m ) có bao nhiêu điểm cực trị?
A. 5
B. 7
C. 9
D. 10
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là

A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0