Gọi H là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy sao cho 2 z - z ¯ ≤ 3 và số phức z có phần ảo không âm. Tính diện tích hình H
A. 3 π
B. 3 π 4
C. 3 π 2
D. 6 π
Gọi H là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy sao cho 2 z - z ≤ 3 và số phức z có phần ảo không âm. Tính diện tích hình H
A. 3π
B. 3 π 4
C. 3 π 2
D. 6π
Gọi (H) là hình biểu diễn tập hợp các số phức z trong mặt phẳng tọa độ Oxy để ![]() số phức z có phần thực không âm. Tính diện tích hình (H).
số phức z có phần thực không âm. Tính diện tích hình (H).
![]()
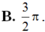
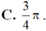
![]()
Chọn A.
+ Giả sử z = a + bi, khi đó ![]() , giả thiết của bài toán là
, giả thiết của bài toán là
![]()
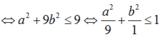
+ Vậy tập hợp các điểm biểu diễn cho số phức z là điểm M(a; b) thuộc miền trong của elip 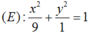 (kể cả các điểm trên biên).
(kể cả các điểm trên biên).
+ Bán trục lớn của ( E) là a = 3, bán trục bé của ( E) là b = 1 nên diện tích cần tính của miền ( H) là S = πab = 3π.
Trong mặt phẳng tọa độ Oxy, gọi (H) là tập hợp điểm biểu diễn số phức w = ( 1 + 3 i ) z + 2 thỏa mãn | z - 1 | ≤ 2 . Tính diện tích của hình (H).
A. 8 π .
B. 12 π .
C. 16 π .
D. 4 π .
Cho số phức z thỏa mãn điều kiện z + 4 + z - 4 = 10 Tập hợp điểm biểu diễn số phức z trong mặt phẳng tọa độ Oxy là một hình phẳng có diện tích bằng
A. 20 π
B. 15 π
C. 12 π
D. 16 π
Xét các số phức z thỏa mãn điều kiện z - 1 + i = 2 Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn các số phức w = z + 2 -i là
A. đường tròn tâm I(-3;2), bán kính R = 2.
B. đường tròn tâm I(3;-2), bán kính R = 2.
C. đường tròn tâm I(1;0), bán kính R =2.
D. đường tròn tâm I(1;-1), bán kính R = 2.
Trong mặt phẳng tọa độ Oxy, cho số phức z thỏa mãn z - 1 + 2 i = 3 . Tập hợp các điểm biểu diễn cho số phức w=z(1+i) là đường tròn
A. Tâm I(3;-1); R = 3 2
B. Tâm I(3;-1);R=3
C. Tâm I(-3;1); R = 3 2
D. Tâm I(3;-1);R=3
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện z + 1 ≤ 2 là
A. Đường tròn I - 1 ; 0 , bán kính R = 4
B. Đường tròn I 1 ; 0 , bán kính R = 2
C. Hình tròn tâm I 1 ; 0 , bán kính R = 2
D. Hình tròn tâm I - 1 ; 0 , bán kính R = 2
Đáp án D
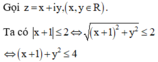
Vậy tập hợp điểm M biểu diễn số phức z thỏa mãn điều kiện đầu bài là hình tròn tâm I(-1;0), bán kính R = 2
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện z + 1 ≤ 2 là
![]()
![]()
![]()
D. Hình tròn tâm I (-1;0) Bán kính R = 2
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện z + 1 ≤ 2 là
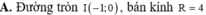
![]()
![]()
![]()