Cho hàm số f(x) là hàm số lẻ, liên tục trên [-4;4]. Biết rằng ∫ - 2 0 f - x d x = 2 và ∫ 1 2 f - 2 x d x = 4 . Tính tích phân ∫ 0 4 f x d x .
A. I = -10
B. I = -6
C. I = 6
D. I = 10
Cho hàm số y = f(x) là hàm lẻ, liên tục trên [-4;4] biết ∫ - 2 0 f - x d x = 2 và ∫ 1 2 f - 2 x d x = 4 . Tính ∫ 0 4 f x d x
A. I = -10
B. I = -6
C. I = 6
D. I = 10
Cho hàm số y = f(x) là hàm lẻ và liên tục trên [-4;4], biết ∫ - 2 0 f - x d x = 2 và ∫ 1 2 f - 2 x d x = 4 . Tính ∫ 0 4 f x d x .
A. I = -10
B. I = -6
C. I = 6
D. I = 10
Cho hàm số y = f(x) là hàm lẻ và liên tục trên [-4;4] biết ∫ − 2 0 f − x d x = 2 và ∫ 1 2 f − 2 x d x = 4 . Tính I = ∫ 0 4 f x d x .
A. I = 10
B. I = -6
C. I = 6
D. I = -10
Đáp án B
Phương pháp:
Sử dụng phương pháp đổi biến và áp dụng công thức
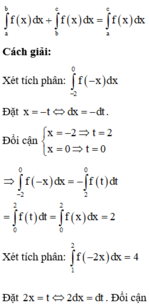
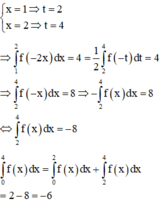
Cho hàm số y = f(x) là hàm lẻ và liên tục trên [-4;4] biết ∫ − 2 0 f − x d x = 2 và ∫ 1 2 f − 2 x d x = 4. Tính I = ∫ 0 4 f x d x .
A. I = -10
B. I = -6
C. I = 6
D. I = 10
Cho hàm số f(x) là hàm số lẻ, liên tục trên [-4;4]. Biết rằng ∫ - 2 0 f ( - x ) d x = 2 và ∫ 1 2 f ( - 2 x ) d x = 4 . Tính tích phân I= ∫ 0 4 f ( x ) d x
![]()
![]()
![]()
![]()
Cho hàm số y = f(x) là hàm lẻ và liên tục trên [-4;4] biết ∫ - 2 0 f ( - x ) d x = 2 và ∫ 1 2 f ( - 2 x ) d x = 4 . Tính I = ∫ 0 4 f ( x ) d x .
A. I = 10
B. I = -6
C. I = 6
D. I = -10
Cho hàm số y = f(x) là hàm lẻ và liên tục trên [-4;4] biết ∫ - 2 0 f ( - x ) d x = 2 và ∫ 1 2 f ( - 2 x ) d x = 4 Tính I = ∫ 0 4 f ( x ) d x
A. I = -10
B. I = -6
C. I = 6
D. I = 10
Cho hàm số y=f(x) là hàm lẻ, liên tục trên [-4;4], biết ∫ - 2 0 f ( - x ) dx = 2 và ∫ 1 2 f ( - 2 x ) dx = 4 . Tính I= 2 ∫ 0 4 f ( x ) dx
A. I = -10.
B. I = -6.
C. I = 6.
D. I = 10
Giả sử hàm số f(x) liên tục trên đoạn [-a; a]. Chứng minh rằng:
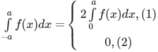
(1) : nếu f là hàm số chẵn
(2): nếu f là hàm số lẻ.
Áp dụng để tính:
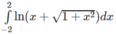
Giả sử hàm số f(x) là hàm số chẵn trên đoạn [-a; a], ta có:
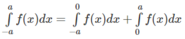
Đổi biến x = - t đối với tích phân
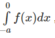
Ta được:
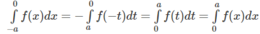
Vậy
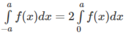
Trường hợp sau chứng minh tương tự. Áp dụng:
Vì 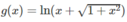
là hàm số lẻ trên đoạn [-2; 2] nên 