Đáp án B
Phương pháp:
Sử dụng phương pháp đổi biến và áp dụng công thức
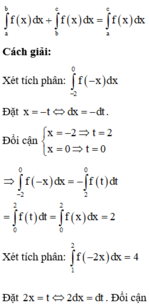
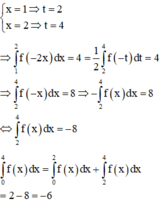
Đáp án B
Phương pháp:
Sử dụng phương pháp đổi biến và áp dụng công thức
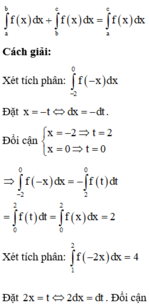
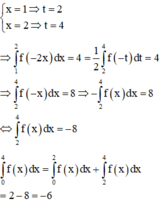
Cho hàm số y=f(x) là hàm lẻ, liên tục trên [-4;4], biết ∫ - 2 0 f ( - x ) dx = 2 và ∫ 1 2 f ( - 2 x ) dx = 4 . Tính I= 2 ∫ 0 4 f ( x ) dx
A. I = -10.
B. I = -6.
C. I = 6.
D. I = 10
Cho hàm số y = f(x) là hàm lẻ và liên tục trên [-4;4] biết ∫ − 2 0 f − x d x = 2 và ∫ 1 2 f − 2 x d x = 4. Tính I = ∫ 0 4 f x d x .
A. I = -10
B. I = -6
C. I = 6
D. I = 10
Cho hàm số y=f(x) có đạo hàm liên tục trên đoạn [ 0 ; 2 ] và thỏa mãn f ( 0 ) = 2 , ∫ 0 2 ( 2 x - 4 ) . f ' ( x ) d x = 4 . Tính tích phân I = ∫ 0 2 f ( x ) d x .
A. I = 2
B. I = - 2
C. I = 6
D. I = - 6
Cho hàm số y = f(x) có đạo hàm liên tục trên R đồ thị hàm số y = f’(x) như hình vẽ.
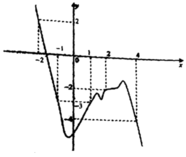
Biết f(2) = –6, f(–4) = –10 và hàm số g(x) = f(x)+ x 2 2 , g(x) có ba điểm cực trị.
Phương trình g(x) = 0?
A. Có đúng 2 nghiệm
B. Vô nghiệm
C. Có đúng 3 nghiệm
D. Có đúng 4 nghiệm
Cho hàm số y = f(x) là hàm lẻ và liên tục trên [-4;4], biết ∫ - 2 0 f - x d x = 2 và ∫ 1 2 f - 2 x d x = 4 . Tính ∫ 0 4 f x d x .
A. I = -10
B. I = -6
C. I = 6
D. I = 10
Cho hàm số y = f(x) là hàm lẻ, liên tục trên [-4;4] biết ∫ - 2 0 f - x d x = 2 và ∫ 1 2 f - 2 x d x = 4 . Tính ∫ 0 4 f x d x
A. I = -10
B. I = -6
C. I = 6
D. I = 10
Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân I = ∫ 0 π 3 f x d x
A. 1/2 + π/3
B. 3 + 1 2
C. 3 - 1 2
D. 1/2
Cho hàm số y=f(x) có f’(x) liên tục trên [0;2] và f(2)=16, ∫ 0 2 f x d x = 4 . Tính I = ∫ 0 2 x f 2 ' x d x
A. I = 7
B. I = 20
C. I = 12
D. I = 13
Cho hàm số y = f ( x ) liên tục trên R và f ( 2 ) = 16 , ∫ 0 2 f ( x ) d x = 4. Tính I = ∫ 0 4 x f ' x 2 d x .
A. I = 144
B. I = 12
C. I = 112
D. I = 28